2013年 浅野中学の問題です。
次の文章を読んで、後の(1)~(5)の問いに答えなさい。
重さの等しい、長さ100cmの2本の棒A、棒Bがあります。2本の棒を図1のように棒の中心に糸をつけて持ち上げると、棒Aはつり合って静止しましたが、棒Bはすぐに傾いてしまいました。棒Bの下になる方の端をCとします。
 図1
図1
ただし、おもりと棒をつないでいる糸、棒を持ち上げるためにつなぐ糸の重さは考えないものとします。
(1)図2のように捧Aの左端に100gのおもりをつるし、左端から40cmのところに糸をつけて持ち上げると、捧Aはつり合いました。棒Aの重さは何gですか。
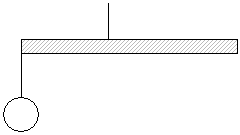 図2
図2
(解説と解答)
棒の長さは100cmですから、左から50㎝のところに重心があります。
左から40㎝のところに糸をつるしていますので、
100×40=10×棒Aの重さになるから、棒Aの重さは4000÷10=400gになります。
(答え)400g
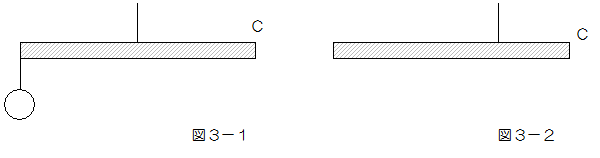
(2)図3-1のように棒Bの左端に160gのおもりをつるし、棒の中心に糸をつけて持ち上げると、棒はつり合いました。次に、おもりを取り除き、糸をつける位置をかえて[図3-2]のようにつり合わせるためには、Cから何cmのところに糸をつければよいですか。
(解説と解答)
棒Bの重心は真ん中にはありません。(1)から棒Bの重さも400gとわかっていますから、中心から右にxcmのところに棒Bの重心があるとすると、
160×50=400×X が成り立ちます。
したがって8000÷400=20cmが棒Bの重心です。重心にひもをつければ水平になるので、したがって50-20=30cmのところでつりあいます。
(答え)30cm
(3)図4のように、棒BのCには160gのおもりを、反対の端にはある重さのおもりDをそれぞれつるします。糸をCから45cmのところにつけ、棒を持ち上げたところ棒はつり合って静止しました。おもりDは何gですか。
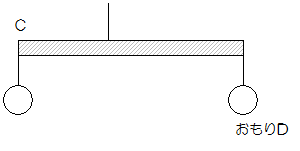 図4
図4
(解説と解答)
糸をつけたところを支点として考えます。重心はCから30cmのところですから、この場合は支点から45-30=15cmです。
したがって支点を中心に反時計回りの回転力は160×45+400×15=7200+6000=13200です。
この回転力をおもりDで支えますから、100-45=55cmがおもりDから支点までの距離になるので、
13200÷55=240gがおもりDの重さになります。
(答え)240g
(4)図5のように、棒BのCには200gのおもりを、反対の端には600gのおもりをそれぞれつるして、棒をつり合わせるためには、Cから何cmのところに糸をつければよいですか。
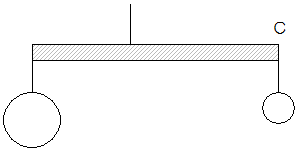 図5
図5
(解説と解答)
支点をCで考えてみましょう。
棒Bの重心はCから30cmのところにありますから、反時計回りの回転力は重心と左端の600gのおもりになるので、
400×30+600×100=12000+60000=72000の回転力があります。
また下向きの力は600+400+200=1200ですから、72000÷1200=60cmで、Cから60cmのところにひもをつるせばよいことになります。
(答え)60cm
(5)(4)の状態で、600gのおもりを水の入ったビーカーの中に沈めると、棒Bは傾き始めました。これは600gのおもりに浮力がはたらくためです。
棒Bにつける糸の位置を棒の中心に移すと、棒Bは図6のように水平に戻りつり合いました。水1cm3あたりの重さを1gとしたとき、600gのおもり1cm3あたりの重さは何gですか。
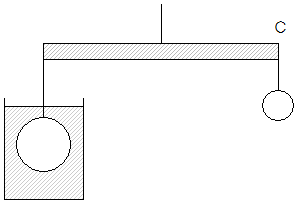 図6
図6
(解説と解答)
棒Bの重心はCから30cmですから、棒の中心からは20cmになるので、この場合、時計回りの回転力は
400×20+200×50=8000+10000=18000になります。
支点から600gのおもりまでの距離は50㎝ですから、18000÷50=360gなので、600-360=240gの浮力がかかっています。
ということはおもりDの体積は240cm3です。(水が1cm3、1gとなっていますから240÷1=240cm3になります。)
したがっておもりDの1cm3あたりの重さは600÷240=2.5gになります。
(答え)2.5g
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
お父さん、気を付けて
==============================================================
中学受験 算数オンライン塾
12月28日の問題
==============================================================
お知らせ
算数5年後期18回 算数オンライン塾「図形の移動(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








