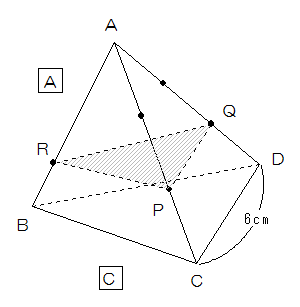
すべての辺の長さが6cmである三角すいABCDにおいて、辺AC、ADをそれぞれ3等分する点のうち点C、Dに近い方をそれぞれ点P、Qとします。
また点Rは辺AB、BC上を動く点とします。ただし、点Rは点Aと点Cには重なりません。
3つの点P、Q、Rを通る平面で三角すいABCDを切ったときにできる2つの立体のうち、点Aを含む立体を 、点Cを含む立体を
、点Cを含む立体を とします。
とします。
(1) 点Rが辺ABのちょうどど真ん中にあるとき、 と
と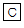 の体積の比を最も簡単な整数の比で答えなさい。
の体積の比を最も簡単な整数の比で答えなさい。
(2)点Rが辺BCを3等分する点のうち点Cに近い方にあるとき、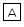 と
と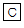 の体積の比を最も簡単な整数の比で答えなさい。
の体積の比を最も簡単な整数の比で答えなさい。
(1)
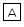 の方は三角すいの
の方は三角すいの
×
×
=
になるので、
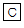 は1-
は1-=
ですから答えは2:7になります。
【答え】2:7
(2)PQRを通る平面とBDの交点をSとするとPQとCDは平行になり、RSとCDも平行になります。
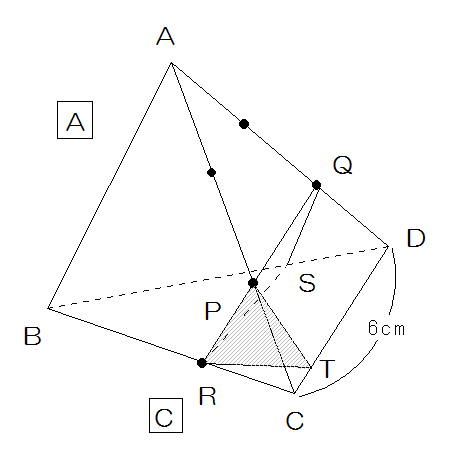
したがって底面は以下のようになり、底面RTUSの部分は三角柱、底面CRTとUSDでひとつの正四面体になります。
正四面体の部分は全体の×
×
=
三角柱の部分は底面を三角すいの断面PRTとすると高さ2cmのすい体がなので、高さ4cmの柱体は
×2×3=
になります。
したがって は
は+
=
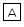 は
は
1-=
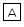 :
: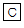 =20:7
=20:7
【答え】20:7
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
誤ったプラス思考
==============================================================
中学受験 算数オンライン塾
7月8日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








