学習院中等科 2011年の問題です。
下の図の三角形ABCで、点Pは辺BCを1:2に分ける点。点Rは辺ACを1:3に分ける点です。APとBRの交点をQとすると、QはAPの真ん中の点になりました。
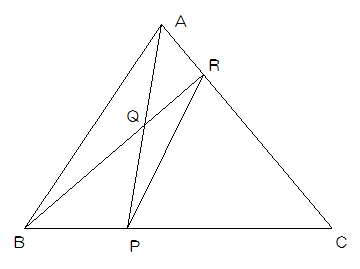
このとき次の問いに答えなさい。ただし、三角形QBPの面積を18㎝2とします。
(1)三角形RPCの面積を求めなさい。
(2)BQ:QRを求めなさい。ただし、最も簡単な整数の比で答えなさい。
AQ=QPは条件になくても、出せるのですが、せっかく条件として出ているのでこれを使って解いていきましょう。
(1)三角形QBP=三角形QBA=18㎝2 BP:PC=1:2なので
三角形APC=18×2×2=72㎝2
AR:RC=1:3より
三角形PRC=72×3/4=54
(答え)54㎝2
(2)三角形ABC=18×2+72=108cm2
三角形ABR=108×1/4=27cm2
三角形ABQ=18㎝2より三角形AQR=27-18=9㎝2
よりBQ:QR=2:1
(答え)2:1
いろいろな解き方がある問題ですので、試してみてください。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
解答用紙と計算用紙
==============================================================
今日の慶應義塾進学情報
自由研究と労作展
==============================================================









