今週は柱体とすい体、さらに回転体について勉強していきましょう。
(1)柱体
ある底面をまっすぐ上に移動していったときにできる立体のことです。三角形をまっすぐ上に移動すれば、三角柱、円をまっすぐに上げれば円柱ということになります。
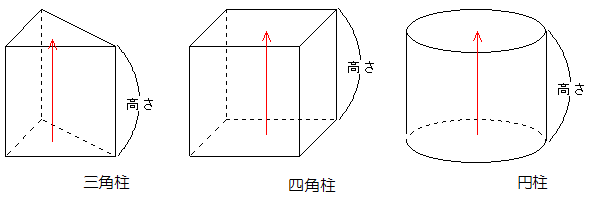
このとき、底面をまっすぐに動かした距離のことを高さといいます。柱体の体積は底面積×高さで求めることができます。
柱体の体積=底面積×高さ
柱体を展開図にしたとき、底面が2つともうひとつ、長方形ができます。
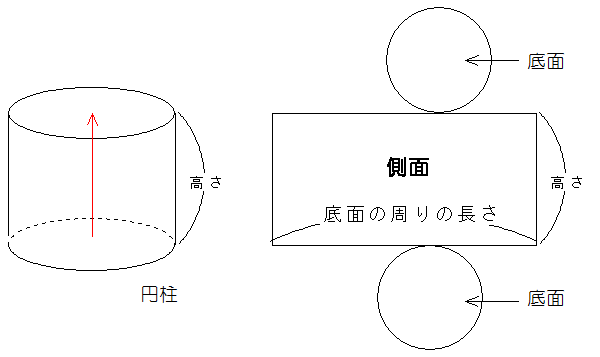
図の右側は、円柱を展開図にしたものですが、底面2つと長方形ができます。この長方形のことを側面といいます。側面の面積のことを側面積といいます。表に出ているすべての面の面積を表面積といいます。
側面席は底面の周りの長さ×高さで求めることができます。
側面積=底面のまわりの長さ×高さ
したがって表面積は底面積×2+側面積になるわけです。
(例題)
半径が6cm、高さ8cmの円柱の体積と表面積を求めなさい。ただし、円周率は3.14とします。
(解説と解答)
半径が6㎝ですから、底面積は6×6×3.14 これに高さをかければよいので、6×6×3.14×8=288×3.14=904.32cm3が体積です。
一方表面積は6×6×3.14×2+6×2×3.14×8=72×3.14+96×3.14=168×3.14=527.52cm2になります。
(答え)体積 904.32cm3 表面積 527.52cm2
(2)すい体
A 角すい
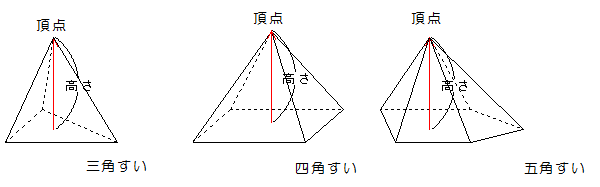
すい体は底面上の1点から垂直線をのばし、その線上の点(頂点)と底面の各点を結んでできる立体のことです。底面が三角形であれば三角すい、四角形であれば四角すいと言います。
頂点と底面の間の長さが高さになります。
すい体の体積は
すい体の体積は底面積×高さ×1/3
です。
なぜ3分の1か、という問題ですが、立方体は実は3つの四角すい(底面は正方形)でできているのです。
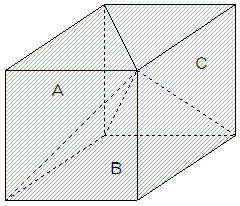
図のようにA、B、C3つの四角すいが立方体の中にちょうど入っていることがわかるでしょう。ここから、すい体の体積は柱体の体積の3分の1という考え方ができるのです。
B 円すい
円すいは底面の円の中心から垂直に伸ばした線上の点と底面をつないだ立体を言います。
頂点から底面の円までの距離はどこでも同じです。この距離のことを母線といいますが、長さが同じですから、側面はおうぎ形になります。
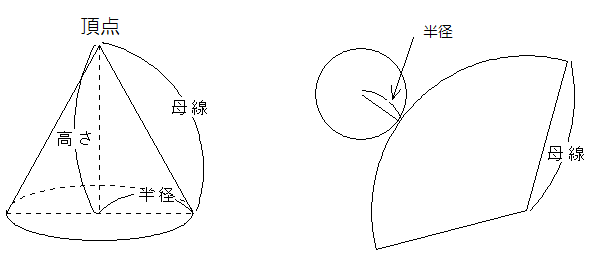
このとき、おうぎ形の弧の長さと底面の円の円周は同じになるので、
半径×2×3.14=母線×2×3.14×中心角/360

という公式が生まれます。
円すいの体積=半径×半径×高さ×1/3
円すいの側面積=母線×半径×3.14
円すいの表面積=円すいの底面積+円すいの側面積=半径×半径×3.14+母線×半径×3.14=(半径+母線)×半径×3.14
ということになります。
底面の半径は6cm、高さ8cm、母線10cmの円すいがあります。これについて次の問いに答えなさい。ただし円周率は3.14とします。
(1)この円すいの体積を求めなさい。
(2)側面の中心角を求めなさい。
(3)この円すいの側面席を求めなさい。
(解説と解答)
(1)公式通りですから、6×6×3.14×8×1/3=96×3.14=301.44cm3
(2)中心角/360=半径/母線 ですから360×6/10=216°
(3)母線×半径×3.14=10×6×3.14=188.4cm2
(3)回転体
ある平面図形を直線を軸にして回転させてできる立体を回転体といいます。
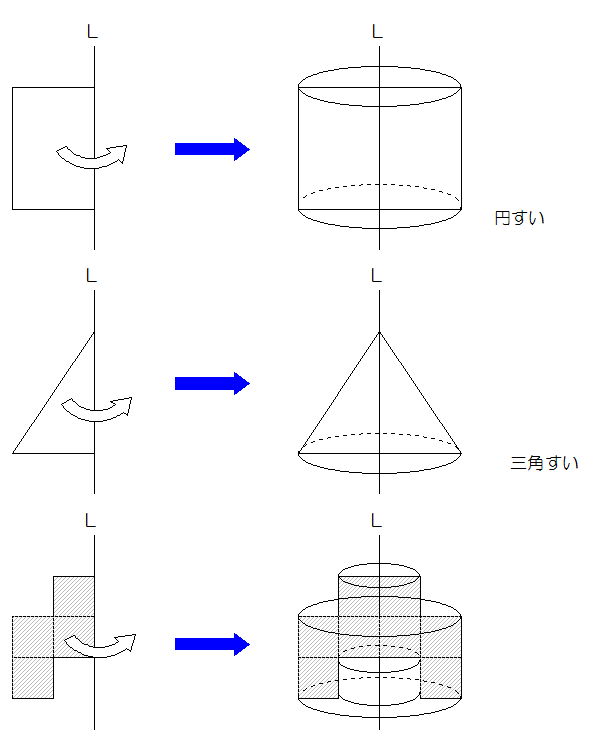
長方形を軸を中心に360°回転させると、円柱になります。
三角形を軸を中心に360°回転させると、円すいになります。
下図のような図形をLを軸にして1回転させてできる立体の体積と表面積を求めなさい。ただし、円周率は3.14とします。
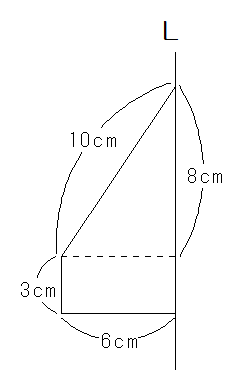
(解説と解答)
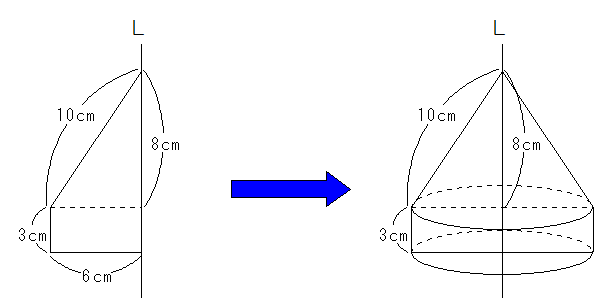
図のようになります。体積は、円柱と円すいの体積の合計です。式を書き切って、最後に3.14の計算をすることにしましょう。
円柱の体積 6×6×3.14×3+円すいの体積6×6×3.14×8×1/3=(108+96)×3.14=204×3.14=640.56cm3
表面積は円すいの側面積+円柱の側面積+円柱の底面積になります。これも式を書き切って、最後に3.14の計算をします。
10×6×3.14+6×2×3.14×3+6×6×3.14=(60+36+36)×3.14=132×3.14=414.48
(答え)体積 640.56cm3 表面積 414.48cm2
最近は立体の問題が増えてきました。例えば直方体と切断したり、立体図形をくりぬいたりしていますが、まず基本はここですから、しっかり公式を覚えてください。
なぜこの公式になるのか、理由も覚えておくと良いでしょう。それを利用して解く問題もありますので、注意しておきましょう。
以下のプリントもお役立ていただければと思います。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
学校の偏差値が落ちるとき
==============================================================
中学受験 算数オンライン塾
5月12日の問題
==============================================================

==============================================================
お知らせ
算数5年前期第16回 算数オンライン塾「速さ(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








