2013年、駒場東邦の問題です。
ある競技では1人の選手の演技に対し、6人の審査員A、B、C、D、E、Fが1から10までの整数で10点満点で点数をつけます。その6つの点数のうち最も高い点と最も低い点を除いた4名分の点数の平均をその選手の得点とし、整数または小数で表します。
ただし、最高点や最低点が複数ある場合はその1名分の点数を除いて計算します。
例えばA5点、B8点、C6点、D9点、E2点、F8点の場合は9と2を除いた平均なので、(5+8+6+8)÷4=6.75よりこのときの得点は6.75点となります。
以下、6人の審査員の点数を順に並べて

のように表記することにします。
 のときは1と4を一つずつ取り除いた平均なので
のときは1と4を一つずつ取り除いた平均なので
(1+3+4+2)÷4=2.5よりこのときの得点は2.5点となります。
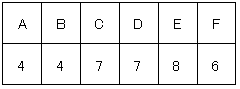 のときは
のときは
(4+7+7+6)÷4=6よりこのときの得点は6点となります。
全員が同じ点数のとき、例えば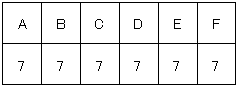 のときは、
のときは、
(7+7+7+7)÷4=7よりこのときの得点は7点となります。
このとき、次の問いに答えなさい。
(1) であるとき、得点を求めなさい。
であるとき、得点を求めなさい。
(2)F以外の5人の点数が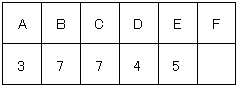 とわかった時、取り打る得点をすべて求めなさい。
とわかった時、取り打る得点をすべて求めなさい。
(3) の得点が5点となるようなB、Cのつけた点数△、□のつけかたが何通りあるかを求めなさい。
の得点が5点となるようなB、Cのつけた点数△、□のつけかたが何通りあるかを求めなさい。
(解説と解答)
(1)最高が10点、最低が2点ですから、(3+5+7+8)÷4=23÷4=5.75が得点になります。
(答え)5.75点
(2)Fの点数が7点以上であれば、(4+5+7+7)÷4=5.75点になります。
F=6点のとき、(4+5+6+7)÷4=22÷4=5.5点
F=5点のとき、(4+5+5+7)÷4=21÷4=5.25点
F=4点のとき、(4+4+5+7)÷4=20÷4=5点
F=3点以下のとき、(3+4+5+7)÷4=19÷4=4.75点
となります。
(答え)5.75、5.5、5.25、5、4.75
(3)得点が5点ですから、4つの合計は5×4=20点です。
7が最大の数であるとすると、BとCと3のどれかが、除外されます。5×2=10点は活かされるので、残りは10点。
Bが除外される場合は(B、C)=(1、7)(2、7)(3、7)
3が除外される場合は(B、C)=(4、6)(5、5)(6、4)
Cが除外される場合は(B、C)=(7、3)(7、2)(7、1)の9通りです。
BかCのどちらかが8以上の数であれば、最大の数は7ではなくなります。
B、C以外の数の合計がちょうど7+3+5+5=20点になるので、もう一つの数は3以下でなければならないことがわかります。
したがってB>Cであれば、
(B、C)=(8、3)(8、2)(8、1)(9、3)(9、2)(9、1)(10、3)(10、2)(10、1)の9通りです。
B<Cでも同じ9通りあるので、合計9×3=27通り
(答え)27通り
やや面倒な問題ではありますが、整理をしていくことで調べることを絞り込んでいくことができるでしょう。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
「わかった!」は危険のシグナル
==============================================================
今日の慶應義塾進学情報
解答欄を確認するくせ
==============================================================

==============================================================
お知らせ
算数5年後期12回 算数オンライン塾「流水算」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








