2013年 浅野中学の問題です。
図1のような三角形ABCがあります。辺BC上に点Dを角BADと角CADの大きさが等しくなるようにとります。また点Cを通りADに平行な直線を引き、この直線が辺BAの延長と交わる点をEとします。
AB=5cm、BC=7cm、CA=4cmとするとき、次の(1)から(3)の問いに答えなさい。ただし、それぞれの比は、すべてもっとも簡単な整数の比で答えなさい。
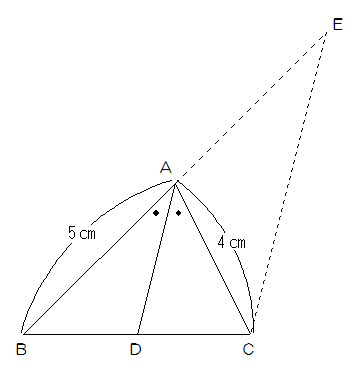 図1
図1
(1)BDの長さ:DCの長さを求めなさい。
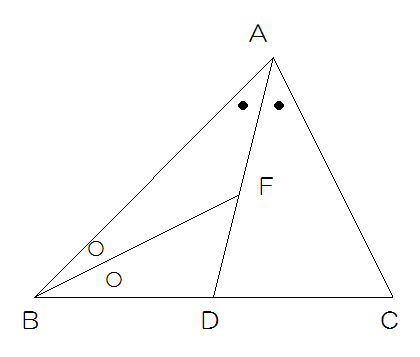 図2
図2
(2)さらに図2のようにAD上に点Fを各ABFと角DBFの大きさが等しくなるようにとります。このとき、DFの長さ:FAの長さを求めなさい。
(3)三角形ABFの面積:三角形BCFの面積:三角形CAFの面積を求めなさい。
(1)この図を見た瞬間、「ああ、角の二等分線の定理ね。」といって5:4と出してしまう生徒がいる、というリスクをこの問題は抱えています。
図1のように角Aを二等分したとき、AB:AC=BD:DCになるというのが「角の二等分線の定理」です。ここまで教えてしまう先生は多分、いるだろうなと思います。
さて、この図1はその証明に使われる図でもあります。
ADとECが平行ですから、角DAC=角ACEとなります。また角BADと角AECも同じになります。(同位角)
したがって三角形ACEは底角が等しいので二等辺三角形となり、AC=AE=4cmとなります。
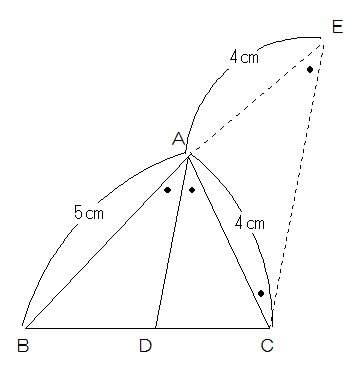 図3
図3
このとき、三角形ABDと三角形EBCは相似ですから、BD:DC=BA:AE(=BA:AC)になるのです。
(答え)5:4
(2)すると図2においてもBD:BA=DF:FAということになるので、BDの長さは7÷(5+4)×5=cmとなるので、DF:FA=BD:BA=
:5=7:9になります。
(答え)7:9
(3)三角形ABF=【9】とすれば、三角形BDF=【7】 BD:DC=5:4 より三角形BCF=【7】÷5×9=【12.6】、三角形CAFは【9】÷5×4=【7.2】
したがって三角形ABFの面積:三角形BCFの面積:三角形CAFの面積=9:12.6:7.2=45:63:36=5:7:4
(答え)5:7:4
こういう問題を練習すれば、間違いなく教える先生は増えるでしょう。きっと。
(もう、教えちゃってるし。)
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
うわさ・・・
==============================================================
今日の慶應義塾進学情報
前夜の宿泊
==============================================================
お知らせ
算数5年後期14回 算数オンライン塾「容器と水量(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








