2014年雙葉中学の問題です。
長方形A、B、Cが一直線上に図のように並んでいます。Cだけが毎分5cmの速さで直線に沿ってA、Bの上を通り、矢印の方向に動いていきます。
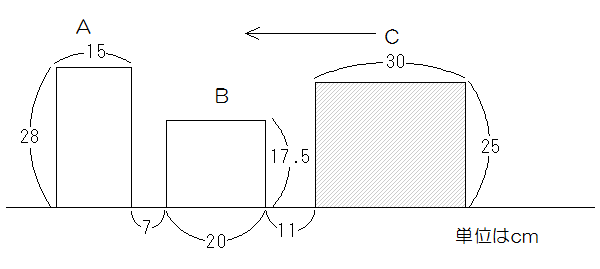
（１）CがA、Bと重なる面積が一番大きくなるのは、Cが動き始めてから何分何秒後ですか。またそのときの面積は何cm2ですか。
（２）CがA,Bと重なる面積が480cm2となるのは、Cが動き始めてから何分何秒後と何分何秒後ですか。
（１）
Cの高さは25㎝なので、Aと重なる最大の面積は15×25＝375cm2
またBと重なるのは20×17.5＝350cm2になります。
Cの先端がAの左端と重なる時、重なる面積は375＋17.5×8＝375＋140＝515
Cの右端がBの右端と重なる時、重なる面積は350＋25×3＝425
425cm2から、1cm進むごとに重なる面積は増えていくのでCの先端がAの左端に重なった時が、最大になることから、
15＋7＋20＋11＝53cm
53÷5＝10.6分後＝10分36秒後
【答え】10分36秒後 515cm2
（２）Cの右端がBの右端に重なった時、425cm2ですから、あと480－425＝55cm2増えればいいことになります。
1cm進むと、25×1－17.5×1＝7.5cm2増えることになるから、55÷7.5＝
30＋11＋
2回目は、Cの左端がAの左端と重なってから、後になります。
AとCが重なる最大値は375cm2なので、480－375＝105cm2がBと重なっていればいいから、
105÷17.5＝6cm分、BとCが重なっていればいいので、Cの右端は20－6＋11＋30＝55cm進んだときですから、
55÷5＝11分後
【答え】9分40秒後 11分後
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
学習計画を練り直す
==============================================================
今日の慶應義塾進学情報
新1年生
==============================================================
==============================================================
==============================================================
にほんブログ村
