2014年 早稲田実業の問題です。
下の図のように、4cm間隔の平行な直線が20本あり、1本目の直線上の点Aから20本目の直線まで2本の直線を引きます。そのときにできる高さが4cmの台形を、上から台形1、台形2、台形3、…、台形18とします。台形1の上底の長さが3cmのとき、次の各問いに答えなさい。
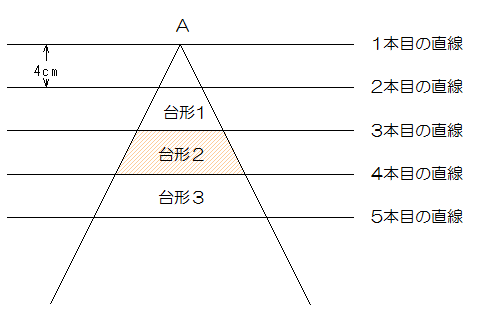
(1)台形2の面積(影の部分の面積)を求めなさい。
(2)台形( ア )の面積は186cm2です。( ア )をうめなさい。
(3)台形1、台形3、台形5、台形7、…、台形17の面積の和を求めなさい。
(1)
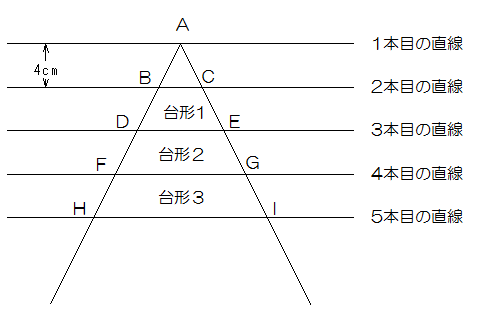
三角形ABC、三角形ADE、三角形AFG、三角形AHIと相似の三角形です。
BC=3cm、DE=6cm、FG=9cm、HI=12cm、となっていきます。
したがって台形2の面積は
(6+9)×4÷2=30cm2
(答え)30cm2
(2)
台形1の上底+下底は9㎝、
台形2の上底+下底は15㎝、
台形3の上底+下底は21㎝、というように6cmずつ増えていきます。
186×2÷4=372÷4=93cm
(93-9)÷6+1=15より台形15になります。
(答え)15
(3)
奇数番の台形の上底+下底は12cmずつ増えます。
1番の上底+下底は9cm
3番の上底+下底は21cm
5番の上底+下底は33㎝・・・
となっていきますから、
17番の上底+下底は12×8+9=105cm
したがって上底+下底の和は(9+105)×9÷2=513になるので、面積の和は
513×4÷2=1026
(答え)1026cm2
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
個の勉強方法
==============================================================
今日の慶應義塾進学情報
体育実技の意味
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








