2010年浦和明の星の出題です。
下の図のように、A地点からC地点へ行くには、途中でB地点を通ります。A地点からB地点に向かう道は上り坂で、B地点からC地点に向かう道は下り坂になっています。また、A地点からB地点までの距離とB地点からC地点までの距離の比は1:2です。
花子さんが、A地点からC地点までを往復したところ、行きが10分、帰りが14分かかりました。
ただし、花子さんの坂道を上る速さ、下る速さはそれぞれ一定であるとします。このとき、次の問いに答えなさい。

(1)花子さんがA地点からB地点までの坂を往復するとしたら、何分かかりますか。
(2)花子さんが坂を上るときの速さと下るときの速さの比を、もっとも簡単な整数の比で表しなさい。
花子さんがA地点を出発するのと同時に、太郎くんがC地点から出発しました。そして、花子さんはC地点までを、太郎くんはA地点までをそれぞれ往復しました。ただし、太郎くんの坂道を上る速さ、下る速さはそれぞれ花子さんと同じとします。
(3)2人が二度目にすれ違うのは、出発してから何分何秒後になるかを求めなさい。
(1)AB:BC=1:2です。したがって
行きの時間はABの距離を上り下りで往復する時間+ABの下りの時間
帰りの時間ははABの距離を上り下りで往復する時間+ABの上りの時間
合計するとABの距離を上り下りで往復する時間の3倍になっていることがわかります。
したがって(10+14)÷3=8分
(答え)8分
(2)14分と10分の差の4分がABの上りの時間と下りの時間の差です。
合計が8分ですから(8+4)÷2=6分が、上りにかかる時間
8分ー6分=2分が下りにかかる時間。
したがって速さの比は逆に上り:下り=2:6=1:3
(答え)1:3
(2)10:7がかかる時間の比ですから速さの比は7:10
(答え)7:10
(3)
2人の動きをグラフにすると以下のようになります。
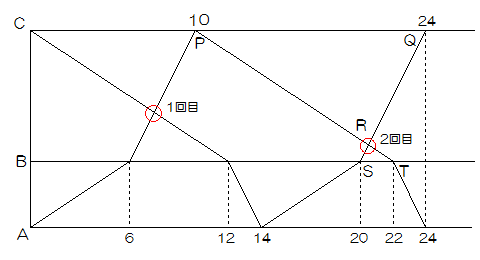
2回目は図のRのところです。
今回はグラフと相似形を利用します。
三角形RSTと三角形PQRは相似形になります。
PQの長さは24-10=14
STの長さは22-20=2
よりSR:RQ=2:14=1:7
SからQまで4分ありますからSからRまでは
4分×1/(1+7)=30秒なので
答えは20分30秒です。
(答え)20分30秒後
グラフを利用すると、どこで会うかは明確にわかるでしょう。
グラフを書く手間の分だけ、最後は相似で簡単に解くことができます。
「映像教材、これでわかる比と速さ」(田中貴)
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
過去問を2段階で解く
==============================================================
今日の慶應義塾進学情報
慶應普通部理科入試傾向
==============================================================
お知らせ
「中学受験、合格して失敗する子、不合格でも成功する子」がパブーでお読みいただけるようになりました。Koboとの連携も後日できるようになりましたら、お知らせします。
詳しくはこちらから
==============================================================










