今回は速さに関する文章題として、通過算と時計算を説明します。
1 通過算
まず最初は通過算です。通過算は長さのあるものが通過していく場合、どのくらいの時間がかかるかということを考えていきます。
1 長さのないものを通過する場合
いま太郎君の前を電車が通過することを考えます。このとき、太郎君は点となり、この前を電車が通過するわけですから、電車の先頭が図のようにAからBまで移動したとき、電車は太郎君の前を通過した、ということになります。
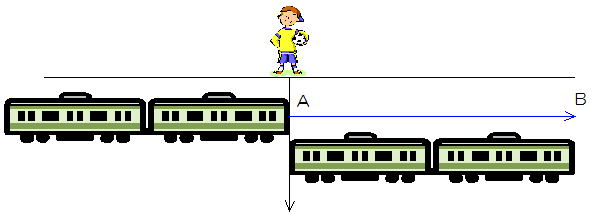
したがって長さがないものを通過する場合は、電車の長さ分だけ先頭が移動すれば通過することになります。
例えばこの場合、電車の長さが200m、電車の時速が36kmであったとき、電車の秒速は36÷3.6=10m*になるので、
200÷10=20秒でこの電車は太郎君の前を通過することになります。
*時速から秒速へ、秒速から時速への計算
1分間は60秒、1時間は60分ですから1時間は60×60=3600秒です。一方時速はkmで表示されることがおおく、1㎞は1000mですから、時速kmを3600÷1000=3.6で割ると秒速mを計算することができます。
一方、秒速mに3.6をかけると時速kmになります。 例えば時速108kmは108÷3.6=30で秒速30mです。また秒速15mは15×3.6=54で時速54kmと計算できます。
2 長さのあるものを通過する場合
今度は電車が鉄橋を通過する場合を考えます。
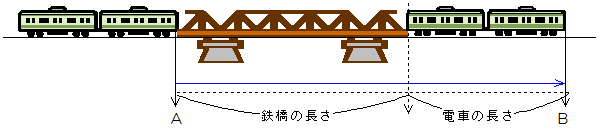
このとき、電車の先頭はAからBまで移動して、鉄橋を通過したということができます。
鉄橋の長さが360m、電車の長さが140m、時速72kmであれば、秒速は72÷3.6=20mですから、
(360+140)÷20=25秒でこの電車は鉄橋を通過することになります。
このように長さのあるものを通過する場合は
(通過するものの長さ+電車の長さ)÷速さ=通過する時間
で通過する時間を計算します。
(例題1)
太郎君の前を8秒、480mの鉄橋を通過するのに32秒かかる電車があります。次の問いに答えなさい。
(1)この電車の時速は何kmですか。
(2)この電車の長さは何mですか。
(解説と解答)
(1)太郎君に長さはないと考えるので、8秒間で電車が移動するのは、電車の長さということになります。
一方、480mの鉄橋を通過するためには、480m+電車の長さを移動しなければならないので、それに32秒かかります。
ということは?
この電車の先頭は480m移動するのに32-8=24秒かかる、ということになるので、秒速は480÷24=20m 時速は20×3.6=72kmになります。
(答え)72km
(2)電車の秒速は20mですから、電車の長さ分を移動するのに8秒かかるので、20×8=160mが電車の長さです。
(答え)160m
3 電車同士が向かい合って通過する場合
今度は電車Aと電車Bが向かい合って通過する場合を考えます。まず、考え方として電車Bには止まっていてもらいましょう。
すると鉄橋の時と同じになるので、電車Aの先頭は図のPからQの位置まで来なければなりません。
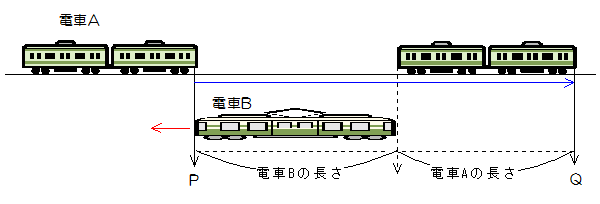
つまり考え方としては鉄橋の時と同じです。この場合電車Aの先頭は二つの電車の長さの和だけ移動しなければならないのです。
では電車Bにも動いてもらいましょう。
そうすると、二つの電車は向かい合っているので、二つの電車の速さの和で近づくことになります。
したがって2つの電車が出会ってからすれ違うまでの時間は
(Aの電車の長さ+Bの電車の長さ)÷(Aの電車の速さ+Bの電車の速さ)
で求めることができます。
この場合、例えばA電車の長さが120m、B電車の長さが180m、A電車の長さが時速72km、B電車の時速が時速36kmとすると、A電車の秒速は20m、B電車の秒速は10mですから。
(120+180)÷(10+20)=10秒間で、すれ違うということになります。
4 電車が追いついてから追い越す場合
今度は電車Aと電車Bが同じ向きに走ります。
電車Aが電車Bに追いついてから追い越すまでの時間を考えてみましょう。同じように電車Bに止まっていてもらうと、電車Aの先頭はPからQまで行かなければなりません。
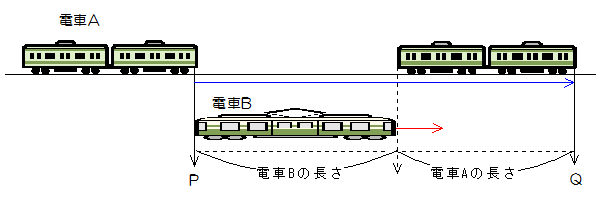
これは向かい合っているときと同じです。ただ、違うのは速さ。電車Aと電車Bは同じ方向に向かっていますから、今度は速さの差で近づきます。
したがって追いついてから追い越すまでの時間は
(Aの電車の長さ+Bの電車の長さ)÷(Aの電車の速さ-Bの電車の速さ)
ということになります。
この場合、例えばA電車の長さが120m、B電車の長さが180m、A電車の長さが時速72km、B電車の時速が時速36kmとすると、A電車の秒速は20m、B電車の秒速は10mですから
(120+180)÷(20-10)=30秒間で、追い越すということになります。
(例題2)
長さが240mの急行列車の時速は108kmです。この急行列車が長さが360mの貨物列車に追いついてから追い越すまで30秒かかりました。
(1)貨物列車の時速は何kmですか。
(2)もしふたつの電車が向かい合って進むとすれば、2つの列車がすれ違うのにかかる時間は何秒ですか。
(解説と解答)
(1)240+360=600mを追い越すのに30秒かかりました。600÷30=20より急行列車の秒速は、貨物列車の秒速より20m速くなります。
急行列車の秒速は108÷3.6=30mですから、貨物列車の秒速は30-20=10 10×3.6=36kmが貨物列車の時速です。
(答え)36km
(2)ふたつの列車の速さの和は30+10=40mになります。したがって向かい合う場合は
600÷40=15秒ですれ違います。
(答え)15秒
2 時計算
さて、次は時計算です。
時計算は、長針が1分間に6度、短針が1分間に0.5度回転することを使って解く問題です。長針は1時間=60分で360度回転し、短針は1時間で360÷12=30度回転するので、長針は360÷60=6 短針は30÷60=0.5
と計算されるわけです。
ではさっそく例題を考えてみましょう。
(例題3)
3時から4時の間を考えます。
(1)短針と長針が重なるのは3時何分ですか。
(2)短針と長針が作る角度が180度になるのは3時何分ですか。
(解説と解答)
(1)下図のように、3時は長針と短針の作る角度が90度になります。(長針は青、短針は赤です。)
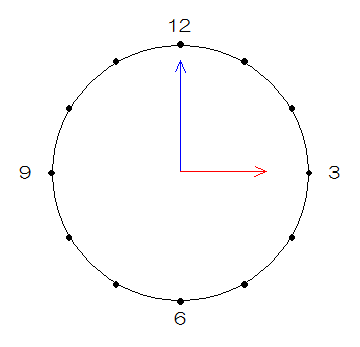
でここから、短針は毎分0.5度で逃げ、長針は毎分6度で追いかけるので、追いつくには
90÷(6-0.5)=90÷5.5==16
分かかることになります。
したがって追いつく時刻は3時16分です。
(答え)3時16分
(2)90度を追いついてから今度は180度開かなければなりません。したがって90+180=270度の差がつかなければなりません。
270÷(6-0.5)=270÷5.5==49
分
(答え)49分
(例題4)
4時から5時の間を考えます。
(1)短針と12の目盛の丁度真ん中に長針がくるはじめの方の時刻は4時何分ですか。
(2)12と長針の間に短針がくるのは4時何分ですか。
(1)問題は短針と12の目盛の間に長針がくるはじめの方の時刻ですから、図のようになります。
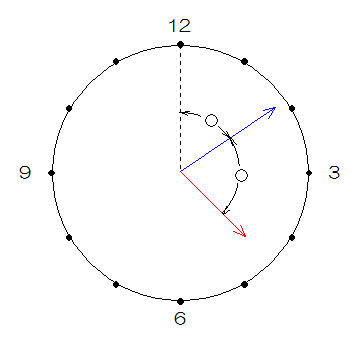
【1】分たったとき、長針は【6】度動き、短針は【0.5】度動きます。
12から4までの目盛は30×4=120度ですから、
120+【0.5】=【6】×2=【12】となるので。
【11.5】=120 【1】==10
分になります。
(答え)4時10分
(2)今度は長針と12の真ん中に短針がくるので、下図のようになります。
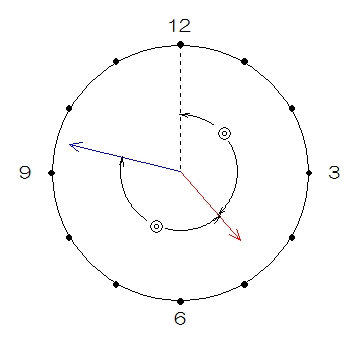
図の◎の角度は12と短針の間ですから120+【0.5】になります。
これの2倍が長針の移動した角度になるので(120+【0.5】)×2=【6】
240+【1】=【6】 【5】=240より 【1】=48
したがって答えは4時48分になります。
(答え)4時48分
ちょっと急ぎ足になってしまいましたが、通過算と時計算についてその考え方を説明しました。
問題文がこれからどんどん複雑になっていくので、しっかり条件を読み取って問題を解いていってください。
以下の教材もお役立てください。
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
満点答案を作ってみる
==============================================================
中学受験 算数オンライン塾
11月10日の問題
==============================================================

==============================================================
お知らせ
算数5年後期11回 算数オンライン塾「通過算・時計算」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








