2013年東邦大東邦の問題です。
半径2cmのおうぎ形4つと、直線を組み合わせてできた下図の図形の内部に半径3cmの円が接しています。この図形の線に沿って円が図形の内部を1周するとき、次の問いに答えなさい。ただし、円周率は3.14とします。
(1)円の中心が動いている線の長さを求めなさい。
(2)この図形の内部で、円が通過しなかった部分の面積を求めなさい。
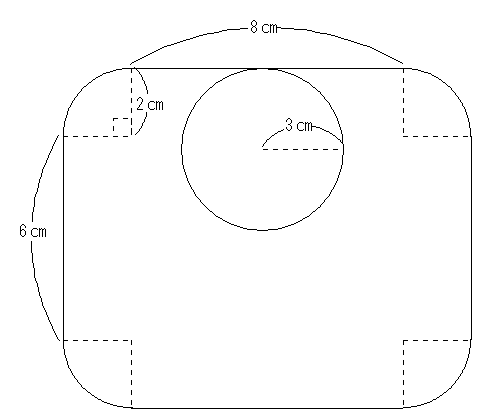
(解説と解答)
(1)図のように動きます。
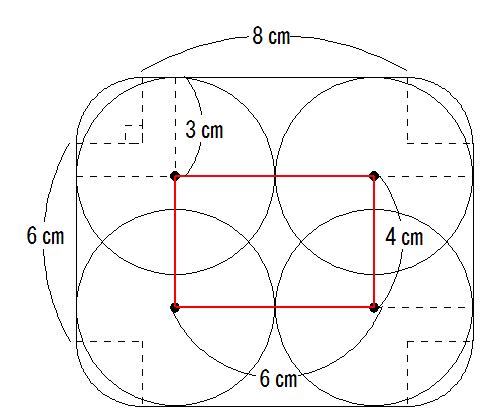
中心は赤い線上を動きますが、横の長さは8+2×2-3×2=12-6=6cm
たての長さは6+2×2-3×2=10-6=4cmですから、合計(6+4)×2=20㎝です。
(答え)20㎝
(2)角のところで、ぶつかってしまうので、下図のオレンジ色の部分は円が通過できません。この4つ分になるので、
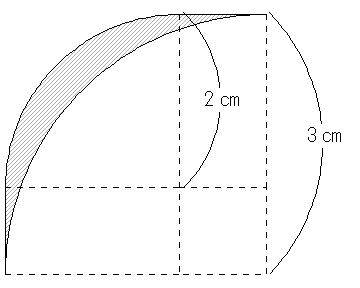
その面積は(2×2×3.14×+2×1×2+1×1-3×3×3.14×
)×4=(1×3.14+5-2.25×3.14)×4=(5-1.25×3.14)×4=20-15.7=4.3
より答えは4.3cm2になります。
(答え)4.3cm2
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
出願に関する注意点
==============================================================
中学受験 算数オンライン塾
11月26日の問題
==============================================================
お知らせ
算数5年後期13回 算数オンライン塾「仕事算」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








