2010年 立教池袋の問題です。
1辺が16㎝の正方形の紙を4回折って小さい正方形にしてから、図の斜線部分が残るように切りました。次の問いに答えなさい。
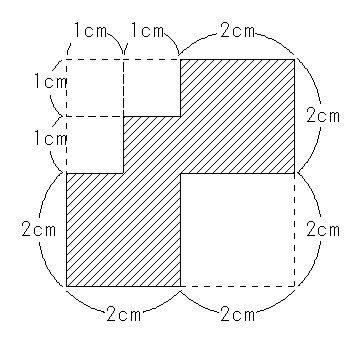 図1
図1
(1)斜線部分の紙を完全に広げてできる図形の面積は何cm2ですか。
(2)斜線部部の紙を完全に広げてできる図形の長さをすべてたすと、何㎝ですか。
それほど難しい問題ではありませんが、上手にもとに戻していきましょう。
頭の中でやろうとせず、手を動かして図にしてしまいます。簡単に書けますから、ここで労力を惜しまないことです。
赤い線を軸に、線対称に折り返します。
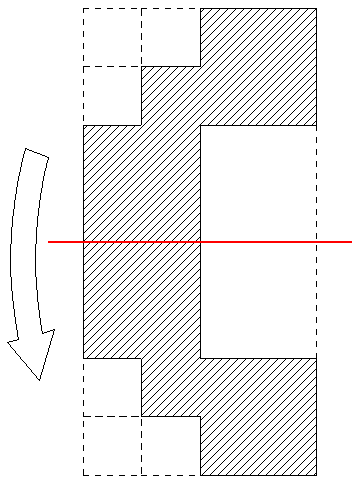 図2
図2
次に今度は青い線を軸に全体を線対称に折り返します。
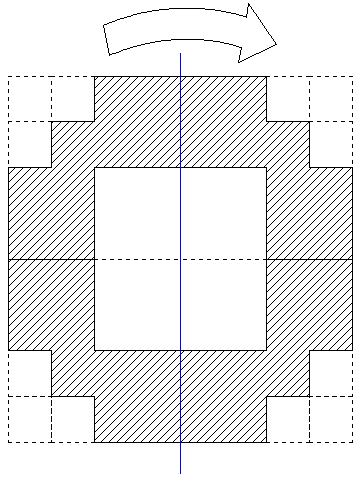 図3
図3
ここまでで2回折り返したので、あと2回ですが、この図形は点対称の図形なので、4つ並べればよいことになります。
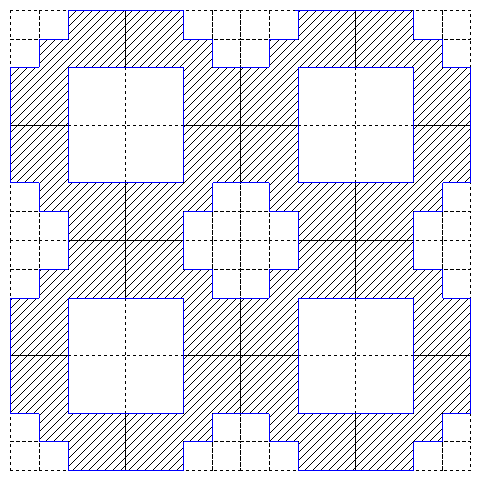 図4
図4
(1)面積は斜線部を16倍するだけですから、2×2×2+1×1×1=9
9×16=144cm2
(2)は図4の青い線を合計すればよいことになります。
外周は16×4+4×4=80cm
内側は4×4×5=80㎝
したがって合計は80×2=160㎝
ということになります。
図が完成すれば、あとは工夫して計算するだけですが、なかなか頭の中だけでこの図を完成させるのは難しいので、しっかり手を動かしてください。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
子どもの解き方に優劣はない
==============================================================
今日の慶應義塾進学情報
慶應ニューヨーク学院説明会
==============================================================









