2010年度、渋谷渋谷の問題です。
容器Aにはスプーン4杯分の醤油が入っています。
容器Bにはスプーン4杯分のみりんが入っています。
まず、容器Aから容器Bにスプーン1杯分の醤油を移す作業をします。…【1】
次に、容器Bをよくかき混ぜてからスプーン1杯分の容器Bの液体を容器Aに移す作業をします。…【2】
次に、容器Aをよくかき混ぜてからスプーン1杯分の容器Aの液体を容器Bに移す作業をします。…【3】
次の問いに答えなさい。
(1)【2】のあとに容器Aに入っているみりんはスプーン何杯分ですか。
(2)【3】のあとに容器Bに入っている液体のうち醤油の割合は何%ですか。
(3)(2)のあとに【2】と【3】の作業を交互に3回ずつ繰り返しました。そのとき容器Aに入っている醤油とみりんの量を最も簡単な整数の比で答えなさい。
スプーン一杯の容量を1としましょう。まず【1】ですが、容器Aから容器Bにスプーン1杯の醤油がいきますからAには醤油が3 Bには醤油が1とみりんが4。
次に【2】に行って、Bから1杯戻ってくるとき、その1杯には1:4で醤油とみりんが含まれますから、Aには醤油0.2とみりん0.8が戻ってきます。したがってAの醤油は3.2 みりんは0.8。逆にBには醤油が0.8、みりんが3.2。
最後に【3】ですが、この段階で容器Aは醤油:みりんが4:1で入っています。
ということはBにもどす1杯には醤油が0.8 みりんが0.2入っているので容器Aの方は醤油が2.4でみりんが0.6.容器Bには醤油が1.6。みりんが3.4となるわけです。
これを表にまとめると以下のようになります。
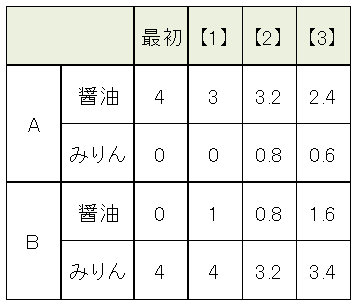
したがって(1)は【2】のあとの容器Aのみりんだから0.8杯分。
(2)は【3】のあとの容器Bの醤油の割合ですから1.6÷5×100=32%になります。
さて問題は(3)
最後の【3】でもAの割合は変わらないので、(2)の後
【2】→【3】→【2】→【3】→【2】で考えればよいことになります。
【2】のときはBからAに1杯移しますが、このときAには3杯分、Bには5杯分残っています。したがってBからAに1杯分移すとBの醤油もみりんも5分の4倍残ります。
【3】をやるときはAにもBにも4杯分残っているので、Aの醤油もみりんも4分の3倍残ります。
そこでその推移は以下の表のようになります。
醤油は4あるので、0.75倍、あるいは0.8倍したあとは、その値を4から引けば、相手の容器にある醤油の量がわかります。
また【2】が終わった時Aの容器の量は4ですから4から醤油の量を引けば、みりんの量になります。
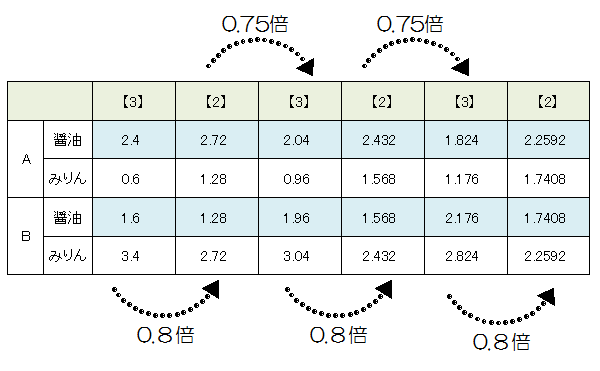
最後Aの醤油:みりん=22592:17408=5648:4352=1412:1088=353:272
(答え)353:272
こういう答えが出ると、ちょっと疑いたくなりますが、表を見直し、計算間違いはしていないことを確認して、自信を持って答えを書きましょう。
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
いろいろなことをやってみたい
==============================================================
今日の慶應義塾進学情報
お弁当
==============================================================

==============================================================
お知らせ
算数4年後期第10回 算数オンライン塾「まとめのテスト」をリリースしました。
詳しくはこちらから
==============================================================








