2009年桜蔭中学の問題です。
下の図のように、正方形のカードを4等分した部分に1から順に整数を書いたものをたくさんつくりました。正方形のカードの大きさはすべて同じです。

(1)上の図の向きで、カードを1枚目から順に左から右に並べました。1枚のカードの上段の2つの数の和が、初めて120より大きくなるのは何枚目のカードですか。
(2)カードを1枚目から50枚目まで、このままの向きで順に重ねました。1枚目の数字1と重なっている1をふくめて50個の数の合計を求めなさい。
(3)1枚目のカードを時計の針の回転と反対向きに90。回転して、2枚目のカードの上に重ねます。次に、1枚目と2枚目を重ねたまま時計の針の回転と反対向きに90。回転して、3枚目のカードの上に重ねます。このようにして50枚重ねたとき、数字3と重なっている3をふくめて50個の数の合計を求めなさい。
(1)N枚目の左上の数は1+4×(N-1)です。その右はそれより1つ大きくなります。
{1+4×(N-1)}×2+1=8×(Nー1)+3>120
ですから
N=15では115 、N=16では123なので、16枚目になります。
(2)左上の数は1から4ずつ増えます。
50番目は1+4×(50-1)=197
(1+197)×50÷2=4950
(答え)4950
(3)
3の下は6になり、次は9、次は16
次は19、22、25、32と4枚ずつの組になります。

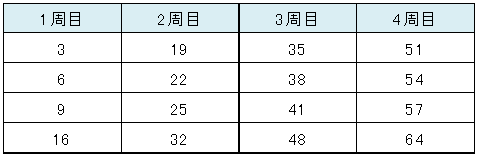
最初の合計は3+6+9+16=34
次の合計はすべて16ずつ増えますから34+16×4=98
50÷4=12…2になりますから
12周目の合計は
34+16×4×11=738
1周目から12周目までの合計は
(34+738)×12÷2=4632
残り2枚は、
3+16×12=195 次は195+3=198です。
したがって合計は
4632+195+198=5025
(答え)5025

「映像教材、これでわかる数の問題」(田中貴)
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
出願準備について
==============================================================
今日の慶應義塾進学情報
併願パターン
==============================================================

==============================================================
お知らせ
算数4年後期第12回 算数オンライン塾「消去算」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村







