2013年駒場東邦の問題です。
1辺の長さが12cmの正方形ABCDがあり、図1のようにBを中心とする半径BDの円と直線BCの延長線との交点をEとします。BEを二等分する点をMとするとき、Bを中心とする半径BMの円をかき、BA、BDとの交点をそれぞれF、Gとします。このとき次の問いに答えなさい。ただし、円周率は3.14とします。
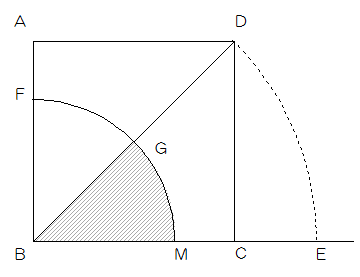 図1
図1
(1)図1の斜線部の面積を求めなさい。
(2)Gを通りABに垂直な直線とABとの交点をHとするとき、GHの長さを求めなさい。
(3)ABを直径とする円をかくとき、図2の斜線部の面積を求めなさい。
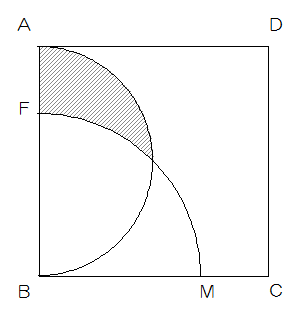 図2
図2
(1)MはBEの中点ですから、おおぎ形BGMとおおぎ形BDEの面積比は1:4です。
角DBCは45°ですから、BD×BD=12×12×2=288
したがっておおぎ形BGMの面積は288×3.14÷8÷4=28.26
(答え)28.26cm2
(2)
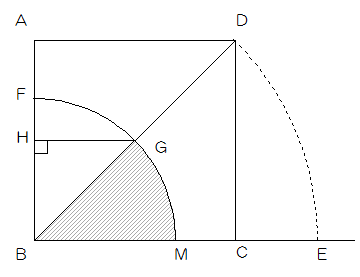 図3
図3
GHはADの半分になるので12÷2=6cm
(答え)6cm
(3)
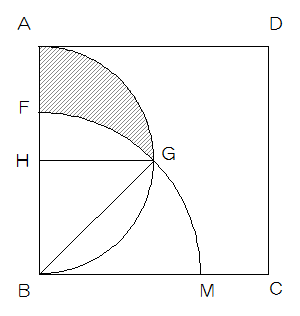 図4
図4
斜線部は4分の1円AHG+直角二等辺三角形HGB-おおぎ形FBGになるので、
6×6×3.14÷4+6×6÷2-9×3.14=18
(答え)18㎝2
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
中学に入って入る塾のメリット
==============================================================
今日の慶應義塾進学情報
樹木と木の実
==============================================================

==============================================================
お知らせ
算数5年前期第4回 算数オンライン塾「割合(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村







