2013年灘中学の問題です。
図のように縦と横の長さの比が1:2の長方形の板を、小さな台の上に、台の左右の板の面積が等しくなるように立ててのせました。すると板は回転することなく、つりあって静止しました。(縦の点線は板を4等分する線、横の点線は板を2等分する線)
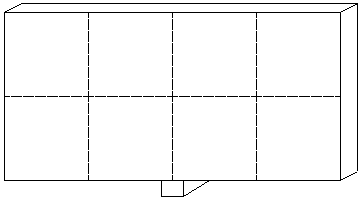
板は台を支点に回転できるものとして、以下の問いに答えなさい。
問1 板を手で支えて、図1のように台の左右の板の面積をそれぞれ半分にするように、板を切り取りました(斜線部分が取り除いた部分)。このとき手をはなすと板はどうなりますか。次のア~ウから選び、記号で答えなさい。
ア 静止し続ける イ 時計回りに回転する ウ 反時計回りに回転する
間2 板を手で支えて、図2のように台の左右の板の面積をそれぞれ半分にするように、板を切り取りました。このとき手をはなすと板はどうなりますか。
問1のア~ウから選び、記号で答えなさい。
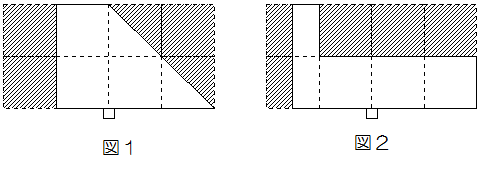
問3 板を手で支えて、図3~図5のように、台の左右の板の面積をそれぞれ半分にするように、板を切り取ったものを3種類作りました。このとき手をはなすとどうなりますか。それぞれ問1のア~ウから選び、記号で答えなさい。
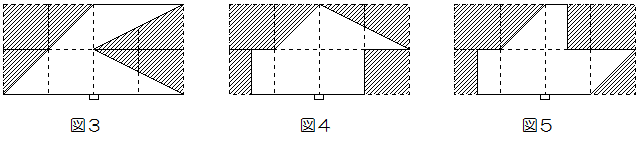
すべての場合で右も左も重さは同じ正方形2枚分です。したがってその2枚分の重心がどこにくるかを考えれば良いことになります。重心が遠い方の回転力が勝りますから左側が遠ければ反時計周りにまわり、右側が遠ければ時計回りになることになります。
図1の場合は、図6のように青い三角形があればつりあいますが、それが右側にずれているので、重心は右側の方が遠くなりますから、時計回りに回ります。
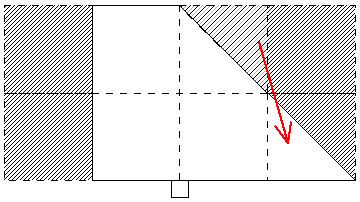 図6
図6
図2の場合は、図7のように青い長方形であればつりあいますが、それが右側にずれているので、やはり重心は右側の方が遠くなりますから、時計回りに回ります。
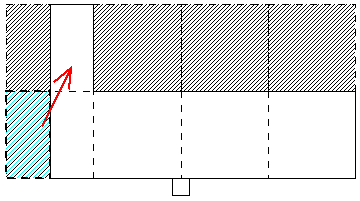 図7
図7
図3の場合は、残った部分で考えると複雑ですが図8のように切り取った三角形で考えるとともに両端の縦の線を底辺として、高さがBO、OCの三角形ですからこの2つの三角形の重心が同じなので、残りの重心も同じになると考えられます。したがってこの場合はつりあいます。
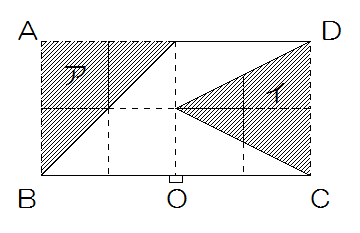 図8
図8
以下のように考えてもいいでしょう。全く同じ三角形を左右にとってみると、残るのはアとイですが、同じ底辺の位置、同じ高さですからアとイの重心の位置はやはり同じになるので、つり合うと考えられます。
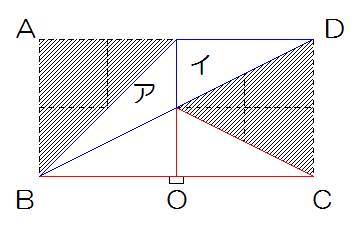
図4の場合は、同じものを図9のように取り除くとウの長方形とエの三角形ではウの長方形の重心が遠くなるので、これは反時計回りに回ることになります。
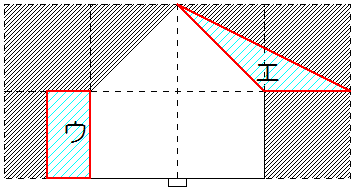 図9
図9
最後に図5ですが、なるべく同じ形を左右に残して切っていくと、図10のようにそれぞれ直角三角形が2つ残ります。これを図のようにずらしてみると、2つの合計はともに同じ重心の位置にあることがわかります。
したがって図5は静止することになります。
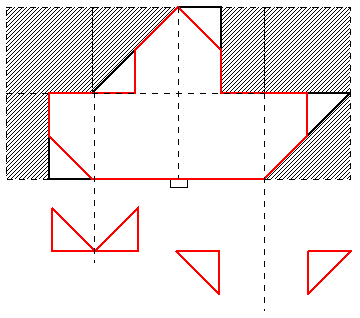 図10
図10
答えは以下の通りです。
(解答)
(1)イ
(2)イ
(3)図3 ア 図4 ウ 図5 ア
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
自分で図を描く
==============================================================
今日の慶應義塾進学情報
慶應進学オンライン 新年度開講しました。
==============================================================

==============================================================
お知らせ
算数5年前期第4回 算数オンライン塾「割合(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








