2013年浅野中学の問題です。
図1のような、1辺の長さ4cmの正方形を底面とし、高さが8㎝の正四角すいA-BCDEがあります。辺ADを2等分する点をPとし、辺AEを2等分する点をQとし、四角形BCPQでこの立体を切断します。次の各問いに答えなさい。
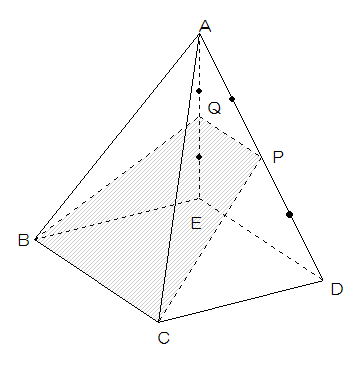 図1
図1
(1)四角形BCPQの面積は何cm2ですか。ただし、図2のような3辺の長さが3cm、4cm、5cmの三角形は直角三角形になります。
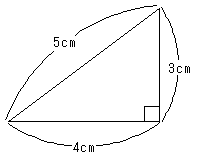 図2
図2
(2)2つに分けられた立体のうち、下側の立体(底面BCDEを含む方の立体)の体積は何cm3ですか。
(解説と解答)
(1)
図3のようにBCの中点をF、EDの中点をG、QPの中点をRとして三角形AFGを考えます。
このとき、FRは台形BCPQの高さになります。
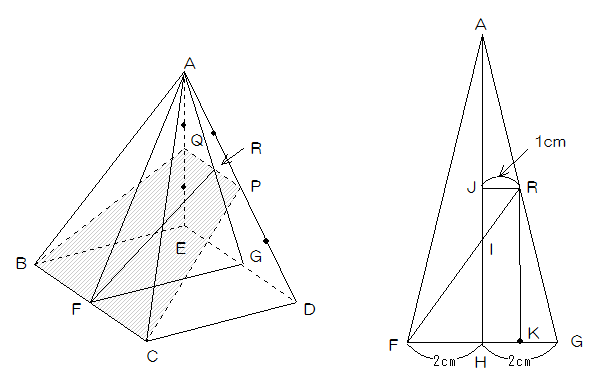 図3
図3
AからFGの中点であるHに垂線を下ろし、FRとの交点をI、RからFGに平行に線を引き、AHとの交点をJとするとAR:RG=1:1ですから、JRの長さは1cmになります。
RからAHに平行に線を引きFGとの交点をKとするとHK=1cm、FK=3cm、RK=JH=8÷2=4cmです。
したがって三角形RFKは3:4:5の直角三角形になるので、FR=5cm
四角形BCPQの面積は(2+4)×5÷2=15cm2になります。
(答え)15cm2
(2)図4のように下の部分を3つに切ります。QP=SM=LO=2cm MD=ES=LC=BO=1cmです。
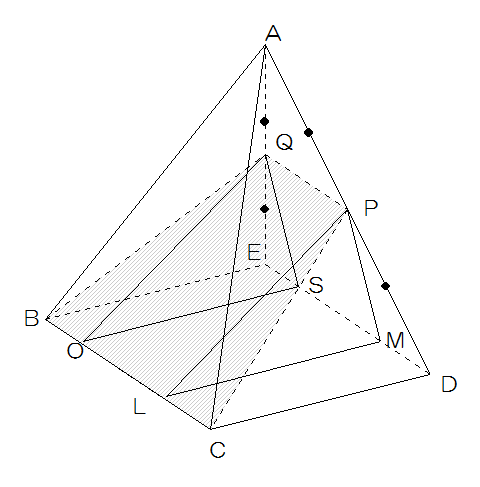 図4
図4
このとき、四角すいP-LCMDと四角すいQ-BOSEは同じになり、体積の合計は4×1×4÷3×2=32/3
真ん中の部分は三角柱となり三角形PLMはLMを底辺としたとき、高さは4cmですから、
4×4÷2×2=16
したがって合計は10 2/3 +16=26 2/3
(答え)26 2/3 cm3
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
いろいろな選択肢
==============================================================
今日の慶應義塾進学情報
願書
==============================================================

==============================================================

==============================================================
お知らせ
算数5年後期第4回 算数オンライン塾「平面図形と比(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








