中学受験　田中貴.com

相似の授業が終わった後、子どもが教室に残って、こんなことを言いました。

「この問題はね、ここにこう線を引くんだ」

多分、本人はそれがその授業で初めてわかったのだろうと思うのです。きっと、それがうれしかったのだろうから、私にそういうことを言ったんだと思います。

しかし、それを聞いていて、私はちょっとした不安を感じました。この子はもしかしたら、それを一つ覚えでやってしまうのではないだろうか？

将棋や碁には定石があります。しかし、定石は試合中、当然変化が起きるわけで、定石通り収まるかどうかはわからない。

入試問題も同じで、「あ、これ、見たことある」と思った瞬間に足元をすくわれることがある。つまり、よくある問題に似せて実は変化を含んでいる。

そういうことは入試問題ではしょっちゅうあります。そして、それを定石通りやって、間違える子どもたちが多いのも事実。

良くパターン問題、といわれるものがあって、それは本当にパターンがあるわけですが、しかし、何でもパターンがあると思ってはいけない。

問題は予断なく、分析を始めないといけないので、「ここは、こう引く」みたいな覚え方をしてはいけないのです。

算数の問題ですべてのパターンを網羅するなど不可能です。だから、考える力そのものをつけないといけない。考える力というのは、変化に対応する力です。

出題がパターン問題から変化しても、そのものをしっかり考えられれば、特に問題はない。

だから、あまりパターンとか、決まった解き方に頼らないことです。

===========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

算数を得意にさせた方法
==============================================================
今日の慶應義塾進学情報

慶應湘南　学校説明会第一日程
==============================================================

==============================================================

==============================================================

にほんブログ村

■　子どもが、どのような勉強を、どう進めているか、を管理することは中学受験ではある意味大事なことです。高校受験や大学受験であれば、それはもう本人がやるしかありませんが、小学生のうちは計画を立てて実行し、その成果を見る、みたいなことを本人が完璧にこなすことは難しい。したがって、やはりお父さん、お母さんの手伝いが必要なのです。

■　しかし、あまりに細かな計画を立て、その進捗状況を注意して、というような管理はお互いにストレスがたまることになります。子どももそろそろ自分でいろいろなことをやりたい年頃ではあるし、反抗期も始まるころなので、良い距離感を持っていないといけない。

■　計画を立てる時から、子どもと一緒に考えることが必要です。例えば塾ではどんな宿題が出ているのか、どの学校を狙うのか、今の現状はどうなのか、ということを勘案しつつ、本人がやる気をもって勉強するように仕向けていかなければならない。「これをやりなさい」と渡して、「やってないの？！」と怒ったところで、それはやはりうまくいくわけがないでしょう。

■　子どもの勉強の管理で最も重要なことは「知る」ことです。子どもが今どんなところに困っていて、その解決のために何をしているのか、を明確に知っている。知っていれば、あとは本人にある程度任せてその進捗状況を後から教えてもらえればいい。

■　それだけでも、子どもたちの勉強はよほど効率的になります。実際に塾では「やりなさい」的なことが多く、みんながやっているから自分もやらなきゃ、みたいなことになりやすいわけですが、それが本人にとって効率的であるかというとそうではない部分も当然あるわけです。だから、そこの取捨選択をしっかり見極めた上で、やるべきことを絞り、なるべくならシンプルにして本人がやりやすいようにしてしまう。例えば、この問題集を全部やる、といっても無理ならだと思うのなら、奇数番号だけやる、というような手も当然考えられるわけです。

■　勉強に充てられる時間は有限ですから、それをいかに効率化するか、やはりいっしょに考えてあげることがこれから重要になってくるので、力を貸してあげてください。

==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

連休が終わったところで
==============================================================
中学受験　算数オンライン塾

5月7日の問題
==============================================================

==============================================================

==============================================================

にほんブログ村

2014年麻布中学の問題です。

1番から9999番までの9999枚のカードを考えます。それぞれのカードには、番号の下にかっこがあり、その中に2つの数が下図のように書かれています。

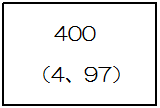
この2つのうち、左の数はカードの番号を99で割った余り、右の数はカードの番号を101で割った余りです。ただし、割り切れるときは0と書かれています、最初の方のカードは下図のようになります。

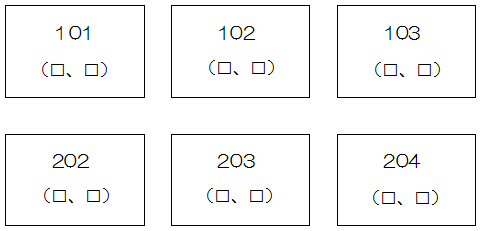
（1）番号が101番、102番、103番、202番、203番、204番のカードの、かっこの中の数をそれぞれ書きなさい。

（2）番号の下に（51、41）と書かれているカードが1枚あります。それは何番のカードですか。

　次に1番から999900番までの999900枚の別のカードを考えます。それぞれのカードには、番号の下にかっこがあり、その中に3つの数が下図のように書かれています。

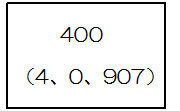
この3つのうち、左の数はカードの番号を99で割った余り、真ん中の数はカードの番号を100で割った余り、右の数はカードの番号を101で割った余りです。ただし、割り切れるときは0と書かれています。

（3）かっこの中の左の数が51、右の数が41であるカードの番号を小さいものから順に3つ書きなさい。

（4）番号の下に（37、15、1）と書かれているカードが1枚あります。それは何番のカードですか。

【解説と解答】
（1)
101÷99＝1･･･2　101÷101＝1　　102÷99＝1…3　102÷101＝1･･･1　　103÷99＝1･･･4　103÷101＝1･･･2
202÷99＝2･･･4　202÷101＝2　　203÷99＝2…5　203÷101＝2･･･1　　204÷99＝2･･･6　204÷101＝2･･･2
【答え】
101→2、0　102→3、1　103→4、2
202→4、0　202→5、1　204→6、2

（2）（1）の答えを見てみると左の数字と右の数字の差は最初の101～103は2、202～204は4と共通になります。
左の数字は0から98まで増えて、右の数字は0から100まで増えるのでその間は差は一定です。
51と41ですから差は10になるので、101から202になるとき99のあまりは2増えていますから10÷2＝5　101×5＝505について考えると
505÷99＝5･･･10　505÷101＝5･･･0より差が10です。
506÷99＝5･･･11　506÷101＝5･･･1で同じく差が10ですから、
99×5＋51＝495＋51＝546　546÷101＝5･･･51で、これが答えになります。
【答え】
546

（3）（2）からまず、546が一番小さな数です。
99と101の最小公倍数は9999です。
9999は左の数が0、右の数も0になります。これは0といっしょです。
10100は左の数が2、右の数が0、10101は左の数が3、右の数が1で差が2になりました。
（1）で101が（2、0）でした。次が10100ですから、9999を加えていけばよいことがわかります。
546の次はしたがって10545となり、その次は20544となります。
【答え】546、10545、10544

（4）37と1ですから、差が36です。101から202になるとき99のあまりは2増えていますから36÷2＝18　18×101＝1818となり
1818÷99＝18･･･36　1818÷101＝18ですから差は36になっています。
したがって最初の数は1818＋1＝1819になります。（1819÷99＝18･･･37　1819÷101＝18･･･1）
1819÷100＝18･･･19ですからこれは答えではありません。
次は9999加えればいいので、
1819＋9999＝11818　11818÷100＝118･･･18
ここで1小さくなったので、最初から4少なくなればいいから、9999を4回加えれば良いことになります。
9999を10で割ると9あまるので、9999を1つ加えるごとに10で割る余りが1ずつ減るわけです。
1819＋9999×4＝1819＋39996＝41815
【答え】41815

「映像教材、これでわかる数の問題」（田中貴）

===========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は

積み重ねることの重要性
==============================================================
今日の慶應義塾進学情報

第二外国語
==============================================================

==============================================================

==============================================================

にほんブログ村