2012年灘中学2日目の2番です。
下の図は、一辺の長さが3cmの立方体で、AMの長さは2cm、ANの長さは1cmです。4つの点A、E、M、Nを頂点とする三角すいをKとします。
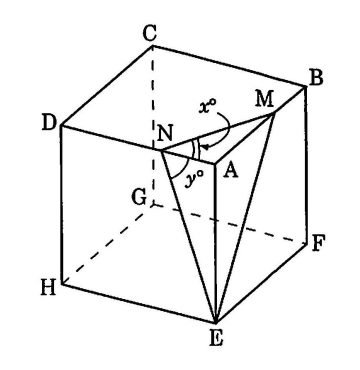
(1)三角形EMNと合同な三角形を1つ、(例)のように(解答)に番き入れなさい。
(2)三角すいKについて、三角形EMNを底面としたときの高さを求めなさい。
(3)図のように、三角形ANMの角Nの大きさをx°で、三角形ANEの角Nの大きさをy°とします。このとき、x°+y°は何度ですか。
(解説と解答)
(1)この問題は着眼点が勝負になるかな、という気がします。
空間を切る問題で、斜めになっている平面を考えなければならないわけですが、斜めになっている平面上でできる三角形をどう描くか?ということを考えなければなりません。
で、注目するのは辺の長さです。
といって小学生ですから平方根は使えません。ただ、直角三角形の斜辺であることはわかります。つまりNMという辺は1㎝、2㎝の直角三角形の斜辺と表すことができます。そこで図にNMを書いてみると
図1 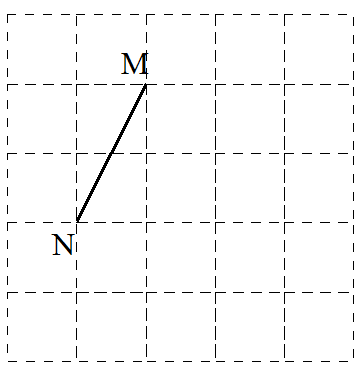
のように書くことができます。次はNEですが、これは1㎝、3㎝の直角三角形の斜辺です。したがって
図2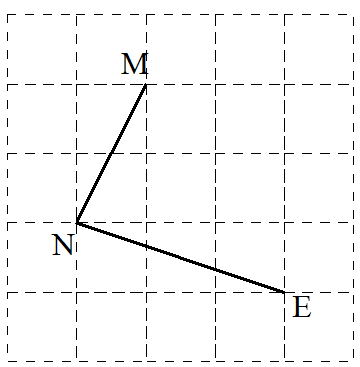
のように作ってみましょう。そうすると最後の辺が2㎝、3㎝の直角三角形の斜辺であればよいので、
図3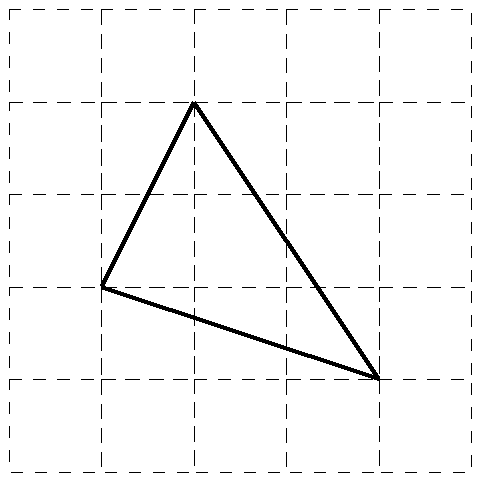
と確認できれば、これが答えになります。
(2)この三角すいの体積は2×1×1/2×3×1/3=1㎝3になります。
で図3からこの三角形の面積を出すことはできますね。1辺3㎝の正方形から1㎝2㎝、1㎝3㎝ 2㎝3㎝の直角三角形を引けばよいので
3×3-1×2×1/2ー1×3×1/2ー2×3×1/2=7/2
になります。底面積×高さ×1/3=体積ですから 7/2×高さ×1/3=1より 高さは6/7㎝ と求めることができます。
(3)はまず展開図を思い起こして、正方形ABCD、ADHE、AEFBを全部同じ平面に書きます。
図4 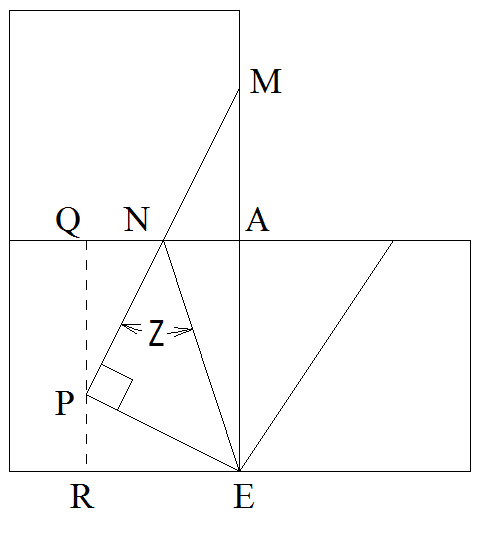
と図4のようになり、図のZの角度がわかればx+yの角度は求められることがわかります。
ここでやはり辺の長さに注目してください。
MNは1㎝2㎝の直角三角形の斜辺でした。同じものをNから下に伸ばしていくと三角形PQNを作ることができます。
この三角形PQNと同じ三角形がありますね。三角形PREです。これも1cm 2cmの直角三角形になります。
ということは三角形NPEは直角二等辺三角形になります。(三角形PQNと三角形PREは合同な直角三角形ですから、角QPNと角RPEの合計は90度です。)
したがってZは45° 180-45=135度が答えになります。
これはピタゴラスの定理を証明する図と同じですね。
図5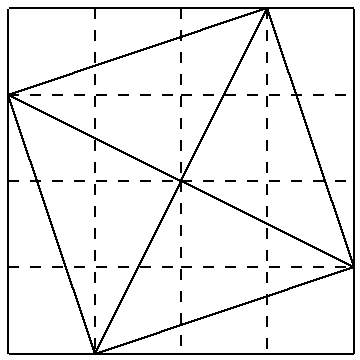
1㎝3㎝の直角三角形を4つ図のように組んでみれば中に正方形ができますが、この正方形の対角線の半分の長さは1㎝2㎝の直角三角形の斜辺です。
中学受験、合格して失敗する子、不合格でも成功する子(アンドロイド版)
中学受験、合格して失敗する子、不合格でも成功する子forkn版
==============================================================
田中貴.com通信を発刊しています。登録は以下のページからお願いします。
無料です。
田中貴.com通信ページ
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
おれって天才じゃん?
==============================================================

「映像教材、これでわかる比と図形」(田中貴)









