2011年 駒場東邦の問題です。
下図のように、変形しない棒が2本、重さが10gの支持台(図の黒い三角形)が4つ、100gのおもりが1つ、はかりが2台あり、棒が水平につり合っています。ここで、おもりは糸で点Bにつるされており、棒と糸の重さは無視できるものとします。このとき、図のAB、BC、DE、EFの間の長さはそれぞれ20cm、20cm、40cm、10cmでした。
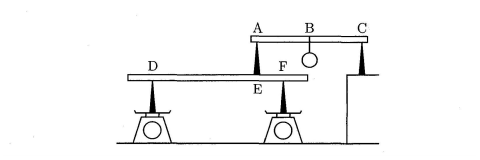
(1)Eには、下向きに何g分の力が加わりますか。
(2)図の右側のはかりの目盛りは何gを指しますか。
それほど難しい問題ではありませんが、ミスがでやすいかもしれません。特に支持台の重さが、抜けやすいかもしれません。
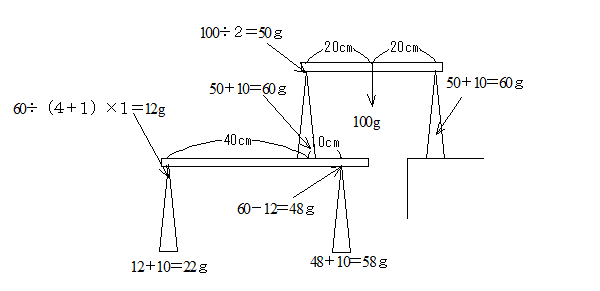
Bにかかる重さは100gでAB=BCですから、Aにかかる重さは100÷2=50gになります。でEにはこの50gに支持台の重さが加わるので
50+10=60g
(1)の答えは60gです。
で、DE:EF=4:1ですからDにはその60gの5分の1がかかる。
逆にFにはその5分の4がかかります。
したがって60×4/5=48g
(念のため図の解説ではDを出して、60から引いています。)
でこれに、支持台の重さが加わるので、右側の台ばかりが示すのは
48+10=58g
でこれが(2)の答えです。
さて、確認をしてみましょう。全体で下向きの重さというのは、100gのおもりと4つの支持台になりますから、合計100+10×4=140gです。
図から左のはかりが、22g 右のはかりが58g そして右の台の下が(1)の答えと同じ60gですから、22+58+60=140g で上向きの力の合計も一致していることになります。
==============================================================
田中貴.com通信を発刊しています。登録は以下のページからお願いします。
無料です。
田中貴.com通信ページ
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
まずは国語の過去問から
==============================================================
今日の慶應義塾進学情報
慶應湘南藤沢高校、全国枠条件変更について
==============================================================








