立体の切断は、子どもたちにとってなかなかイメージがつかめないテーマでしょう。
たとえば、こんな問題。
1辺12㎝の立方体があります。PとQは各辺の中点です。この立方体を点PQRを通る平面で切るとき、頂点Aを含む立体の体積を求めなさい。
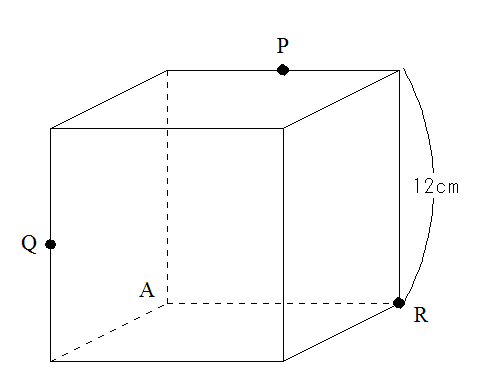
良くある問題だと思いますが、まず初学の段階で間違いやすいのは、立方体の中を通る線を書いてしまうこと。
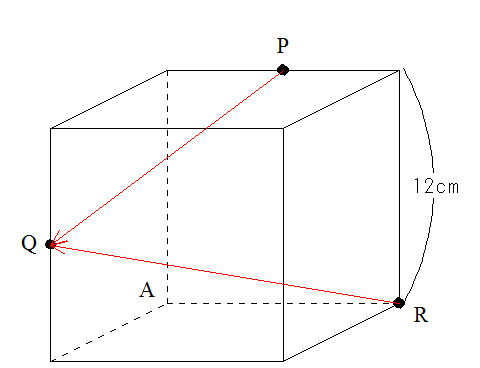
こういう線を書いてしまうと、よくわからなくなります。立体の中をつきぬける線は確かにこの3点を通る平面上にはあるのですが、その面をイメージにしくいのです。
ではどうするか?
この問題では立方体の面上にPとRがあるので、まずこれを結びます。
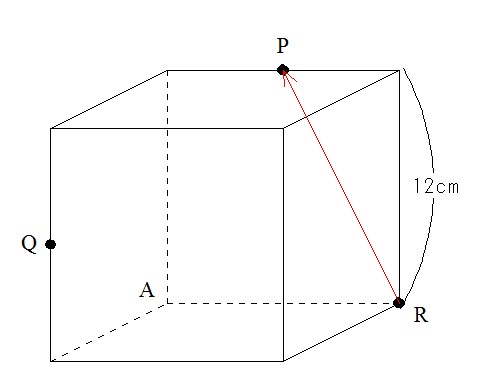
次に、PとRがある平面上をQがある立方体の平面まで、線を伸ばしていきます。この平面との交点をBとしましょう。
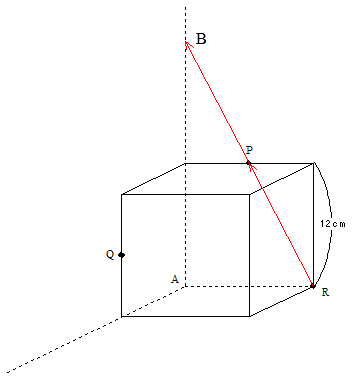
そうするとBとQがある平面に来ましたから、今度はBとQを結びます。
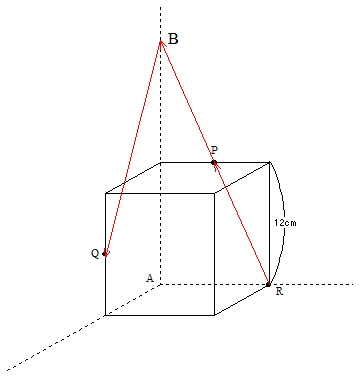
しかしQとRは立方体の作る面上にはいないので、Rがいる立方体の面上までこれを伸ばします。この交点をCとします。
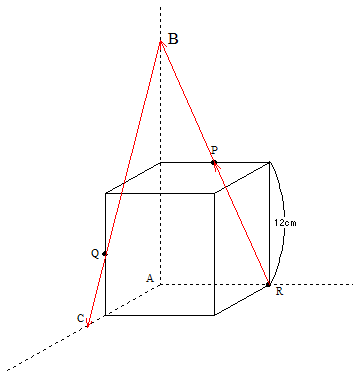
最後にCとRを結ぶと、3点PQRがいる平面と立方体の面との関係が明確にわかるようになります。
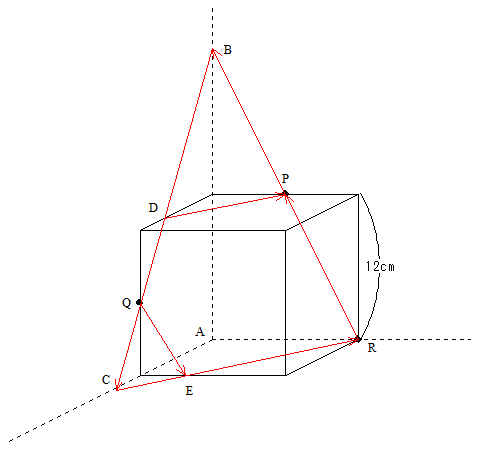
さて、説明のために各点に記号を入れましょう。
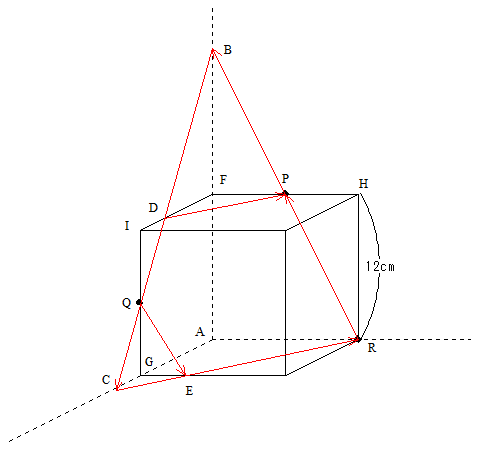
求める立体は三角すいACRBから三角すいFDPBと三角すいCGEQを引けば良い、ということがわかります。
しかもこの3つの立体は、相似形になっています。
FP=PHですからBF=12㎝
IQ=6㎝ですからID:DF=6:12=1:2になるのでDF=12×2/3=8㎝になります。
三角すいACRBは三角すいFDPBの2倍ですから、AC=16cm です。
さて三角すいACRBの高さは24cm 三角すいFDPBの高さは12㎝ 角すいCGEQの高さは6㎝ですから
長さの比が4:2;1
ということは体積の比は
4×4×4:2×2×2:1×1×1=64:8:1
したがって求める体積は三角すいACRBの64分の(64-8-1)で55/64ということになります。
よって
16×12×1/2×24×1/3×55/64=660㎝3
ということになります。
もちろん各三角すいの底辺の長さなどを出して計算してもかまいません。
長くなりましたが、ポイントは切断面のイメージを立方体の平面と合わせて考えることです。
立方体の中をつっきる線を書いてしまうと、イメージが湧きにくくなるので、以上のように立方体の持つ平面上に伸ばしてイメージを作ってください。
これは練習が必要だと思いますので、自分で図を描きながら確認をしていきましょう。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
進学ガイド
==============================================================
今日の慶應義塾進学情報
慶應義塾横浜初等部
==============================================================










