2013年駒場東邦の問題です。(一部問題を省略しました。)
次の【実験1】、【実験2】について、以下の問いに答えなさい。答の値が整数にならない場合は、四捨五入して整数で答えなさい。
【実験1】
2つのはかりA、Bを用意し、それぞれに重さが100gの支持台(図の黒い三角形)を固定しました。
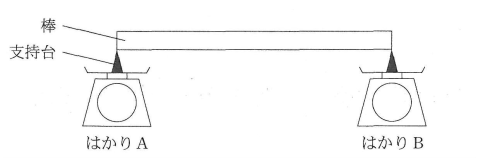 図1
図1
図1のように、重さが600g、長さが60cmの太さが均一な角棒(直方体の棒)の両端を、はかりA、Bの支持台に載せ、水平に支えたところ、はかりA、Bはどちらも400gを示しました。はかりBを支持台とともに、棒の右端から少しずつ左側へ動かし、棒を支える位置を変えていくと、はかりBが示す値は表に示すように変化し、動かした距離が30cmを超えたところで、棒は傾いて落ちました。棒を支える支持台の高さは、はかりの値によらず、常に同じであるとします。
表 はかりBを動かした距離とはかりBが示す値との関係

(1)図2のように、はかりBを棒の右端から20cm動かし、棒の右端におもりを吊るすとき、おもりの重さが何gより大きいと、棒は傾いて落ちますか。
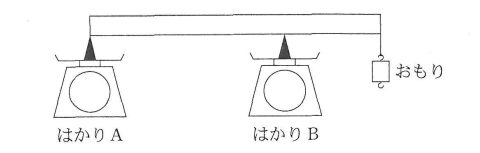 図2
図2
(2)図2のおもりの重さが、(1)で求めた大きさのとき、はかりA、Bはそれぞれ何gの値を示しますか。
(1)
最初の段階で、AとBには400gずつの重さがかかっています。支持台の重さがそれぞれ100gですから、棒の重さは
400×2-100×2=600gです。
問題でBを動かした距離が30㎝のとき、Aは100g、Bは700gでした。
Aは支持台の重さだけですから、棒の重さはAにはかかっていません。逆にBには700gかかっているので、支持台の重さを引くと
700-100=600gで棒の重さはすべてBにかかっています。したがって棒の重心は真ん中にあります。
Bを左に20cm動かしたとき、表ではBは550gでした。そのときAは800-550=250gを示します。
支持台の重さを引くとBは450g、Aは150gになっています。
BとAの距離は40cm、おもりとBの距離は20cmですから、40×150÷20=300gでおもりが300gでちょうどつりあいます。
したがって、300gを超えると棒は傾いて落ちることになります。
(答え)300g
(2)
支持台の重さを考えなければ棒の重さとおもりの重さはすべてBにかかることになります。
したがって支持台の重さを加えると300+600+100=1000gがB。
Aは支持台の重さだけですから100gになります。
(答え)A 100g B 1000g
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
学校別対策コース
==============================================================
中学受験 算数オンライン塾
6月15日の問題
==============================================================

==============================================================
お知らせ
算数5年前期第19回 算数オンライン塾「旅人算とグラフ(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








