今回は点の移動について学習していきます。まずは基本的な問題をしっかりマスタ-してください。
(例題1)
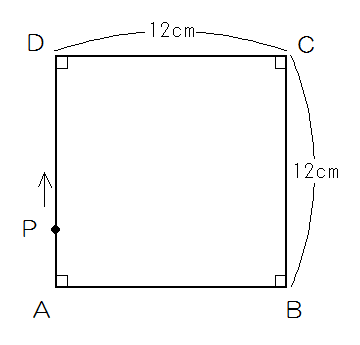
1辺が12㎝の正方形の辺上をAから点Pが毎秒1cmの速さでA→D→C→Bと進んでいきます。三角形APBの面積が正方形ABCDの3分の1になるのは何秒後と何秒後ですか。
(解説と解答)
12×12=144 144÷3=48cm2ですから、APの高さは48×2÷12=8㎝ということになるので、BPの長さが8㎝のときも3分の1になることになります。
したがって最初は8÷1=8秒後
もう1回は12×3-8=28cmですから28÷1=28秒後です。
(答え)8秒後 28秒後
(例題2)
点PはAから、点QはCから同時に出発して矢印の方向に長方形ABCDの辺上を移動します。点Pの速さは毎秒1cm、点Qの速さは毎秒2cmです。
次の問いに答えなさい。
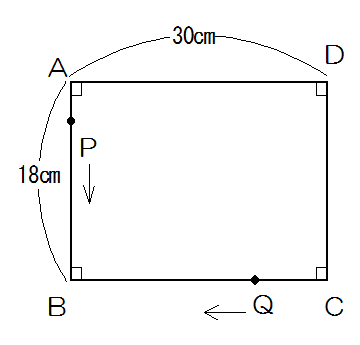
(1)2点が初めて重なるのは出発して何秒後ですか。
(2)出発して28秒後の三角形PBQの面積は何cm2ですか。
(解説と解答)
(1)間の距離は18+30=48cm 2点の速さの和は1+2=3cmですから48÷3=16秒後
(答え)16秒後
(2)Pは1×28=28cmですから、28-18=10㎝でBから10㎝のところにいます。
またQは2×28=56cmですから、56-30-18=8㎝で、Aから8㎝のところにいます。
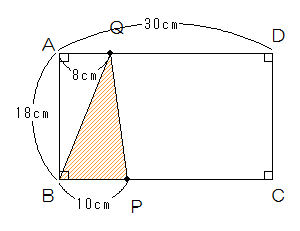
したがって三角形PBQの面積は10×18÷2=90
(答え)90cm2
(例題3)
図のような台形の辺上を点PはAから、点QはCから同時に出発します。
点Pの速さは毎秒1cm、点Qの速さは毎秒3cmです。
次の問いに答えなさい。
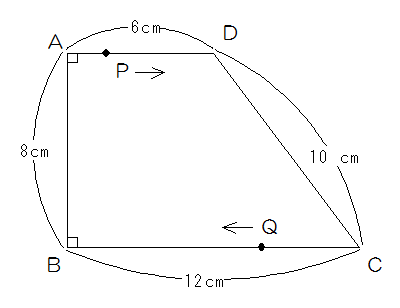
(1)直線PQが直線ABとはじめて平行になるのは何秒後ですか。
(2)直線PQが直線CDとはじめて平行になるのは何秒後ですか。
(3)四角形ABQPの面積が初めて台形の半分になるのは何秒後ですか。
(解説と解答)
(1)APとBQの長さが等しくなれば直線ABと直線PQは平行になります。
したがって12÷(1+2)=4秒後
(答え)4秒後
(2)PDとCQの長さが同じになれば、直線PQは直線CDと平行になります。
AP:CQ=1:2より
6-【1】=【2】ですから【3】=6より【1】=2cmになるので、
2÷1=2秒後
(答え)2秒後
(3)APとBQの和が6+12=18㎝の半分になれば、台形の半分になります。
AP=【1】とするとBQ=12-【2】より AP+BQ=【1】+12-【2】=12-【1】=9より【1】=3
3÷1=3秒後
(答え)3秒後
(例題4)
図のような台形ABCDがあります。点PはCを出発して、矢印の方向へ一定の速さで辺上をBまで動きます。
グラフは、点Pが出発してからの時間と三角形PBCの面積の関係を示したものです。これについて次の問いに答えなさい。
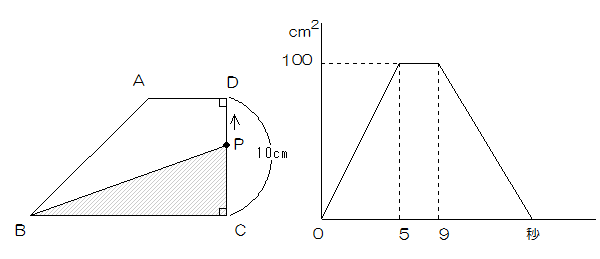
(1)辺BCの長さは何cmですか。
(2)点Pの動く速さは毎秒何cmですか。
(3)三角形BPCが初めて台形ABCDのになるのは何秒後ですか。
(解説と解答)
(1)グラフから三角形BCDの面積が100㎝2ですから、
100×2÷10=20cmがBCの長さです。
(答え)20cm
(2)5秒間でCからDまで10cm移動したので、10÷5=2cm
(答え)2cm
(3)AD間は9-5=4秒ですから、AD=2×4=8cmです。
したがって台形ABCDの面積は(8+20)×10÷2=140cm2です。
三角形BPCの面積が140×=60cm2になるときですから、
60×2÷20=6cm 6÷2=3秒後
(答え)3秒後
(例題5)
図1のような台形ABCDがあります。点PはAを出発して、毎秒1cmの速さで辺上を矢印の方向にCまで動きます。図2は、このときのPが動き始めてからの時間と、三角形PCDの面積の変化のようすを表したものです。これについて次の問いに答えなさい。
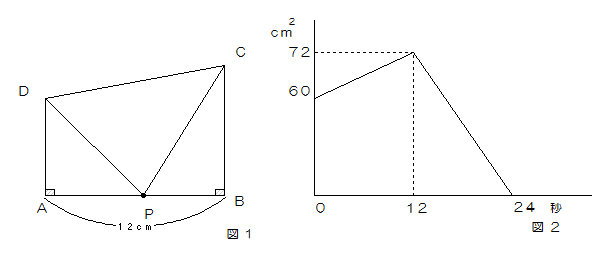
(1)辺AD、BCの長さはそれぞれ何cmですか。
(2)三角形PCDの面積が66cm2になるのは、点Pが動き始めてから何秒後と何秒後ですか。
(解説と解答)
(1)グラフから三角形ADCの面積が60cm2、三角形BCDの面積が72cm2であることがわかります。
60×2÷12=10cm・・・AD 72×2÷12=12・・・BC
(答え)AD 10cm BC 12㎝
(2)グラフから0秒から12秒間の間に72-60=12㎝2の面積が増えていますから、12÷12=1cm2の面積が毎秒増えるので、
(66-60)÷1=6秒後・・・1回目
次に12秒後から24秒後に72cm2へりますから、72÷12=6cm2 が1秒間に減る面積なので、72-66=6
6÷6=1秒後より12+1=13秒後
(答え)6秒後 13秒後
(例題6)
点Aから同時に点P、Qが円周上を矢印の方向に移動します。
Pは1周12秒、Qは1周24秒かかります。このとき次の問いに答えなさい。
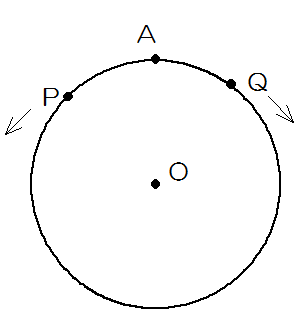
(1)最初に2点が重なるのは何秒後ですか。
(2)最初に円の中心0と点P、Qが一直線になるのは何秒後ですか。
(解説と解答)
(1)角速度で考えます。Pは360÷12=30°が秒速になり、Qは360÷24=15°が秒速になります。
したがって重なるのは360÷(30+15)=8秒後
(答え)8秒後
(2)一直線になるのは、2つの点の間の角度が180°になるときですから、
180÷(30+15)=4秒後
(答え)4秒後
点の移動は速さと相似形が合わさったようなテーマなので、いろいろな応用問題が入試では出題されています。
しっかり自分で図を描いて、どの位置にいるのか、どういう図形ができるのかをしっかりイメージしてから解いていくと良いでしょう。
以下のプリントもお役立ていただければと思います。
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
決めたことをやる能力
==============================================================
中学受験 算数オンライン塾
12月22日の問題
==============================================================
お知らせ
算数5年後期18回 算数オンライン塾「図形の移動(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








