2012年 聖光学院の問題です。
高速道路上を2台の車P、Qが走っていて、QがPを後ろから追いかけています。
QにはPとの距離を測定する機械がついていて、QがA地点を通過したとき、2台の車の距離は600mでした。また、QがPに追いついた場所をB地点とします。
A地点とB地点の途中のC地点とD地点の間は、工事区間のため、2台ともそれ以外の区間の( ア )倍の速さで走行します。QはA地点を通過してから、ちょうど2分後にB地点を通過しました。
図2は、QがA地点を通過してからB地点を通過するまでの2台の車の距離と時間の関係を表したグラフです。このとき、次の問いに答えなさい。ただし、A地点とB地点の間の道路は直線であり、2台の車はC地点とD地点を通過するとき以外は、速さを変えないものとします。また、車の大きさは考えないものとします。
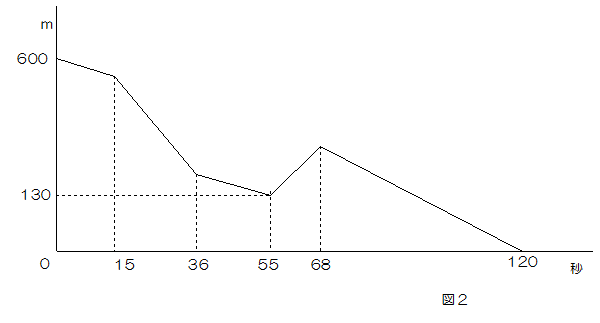
(1)Qが工事区間を通過するのに何秒かかりましたか。
(2)工事区間を走ったときのPとQの速さの比を最も簡単な整数比で答えなさい。
(3)Qが工事区間以外を走ったときの速さは毎秒何mですか。
(4)( ア )にあてはまる数を求めなさい。
(解説と解答)
2台の動きは、下図のようになります。
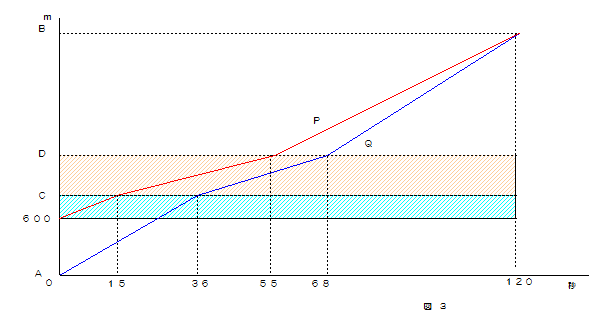
15秒後 → Pが工事区間に入る。Pが遅くなるので、差がさらにつまり始める。もともとQの方が速いのです。
36秒後 → Qが工事区間に入る。
55秒後 → Pが工事区間を出る。差が広がり始める。
68秒後 → Qが工事区間を出る。差が縮まる。
ということになります。
したがって
(1)Qが工事区間を通過するのには68-36=32秒間かかりました。
(答え)32秒間
(2)Pは55-15=40秒間かかっていますから、同じ距離をP:Q=40:32=5:4の時間で動くので速さの比は4:5になります。
(答え)4:5
(3)もとの速さもP:Q=4:5です。
PはQがAを通過したときから、PがCに到着するまで15秒かかっていますから、同じ距離(図3の水色の部分のたての長さです。)をQは
15÷5×4=12秒でいきます。したがって600mを36-12=24秒でいきますから、秒速は
600÷24=25mになります。
(答え)25m
(4)Pの速さは25÷5×4=20mです。
55秒後に図2から2台の車の差は130mでした。したがってその130mをQは68-55=13秒で移動していますから、秒速は
130÷13=10mになっているので、10÷25=0.4がアの値になります。
(答え)0.4
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
重ね着作戦
==============================================================
中学受験 算数オンライン塾
1月7日の問題
==============================================================
お知らせ
算数5年後期18回 算数オンライン塾「図形の移動(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








