2012年の渋谷幕張の問題です。
下の図のように、正方形のマスをたてに3個、よこに5個並べて長方形を作り-ます。この長方形の1本の対角線は、斜線の7個のマスを通過します。
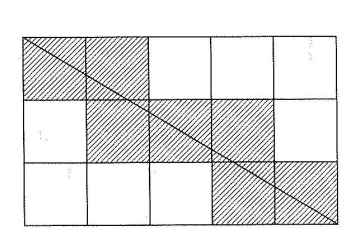
次の各問いに答えなさい。
(1)正方形のマスをたてに7個、よこに11個並べた長方形を作るとき、この長方形の対角線は、何個のマスを通過しますか。
(2)正方形のマスをたてに39個、よこに51個並べた長方形を作るとき、この長方形の対角線は、何個のマスを通過しますか。
最近、よく見かける問題になりました。
例の場合で考えると、3と5ですから互いに素の関係にあります。したがって対角線は左上から右下に行くまでの間に格子点(正方形の頂点)は通過しません。
そうすると内側の線は全部で縦が4本、横が2本ありますから、対角線が通過するごとに1つの正方形が切られていきます。つまり6個切られて、最後に頂点に到達するときにもう1個切られるので合計7個になります。
で(1)ですが、7と11ですから、互いに素です。
そうすると内側の線は縦の線が10本、横の線が6本ですから10+6+1=17です。
で、問題は「対角線が通過する」といっています。もし17で答えが良いのであれば「1本の」と問題に書くべきであって、それが抜けていることを考えると両方の対角線について答えを出せ、という問題ではないかと思います。
そこで説明を簡単にするために、この場合の正方形の長さを7とします。そうすると内側の最初の横の線は11が切られ、22、33、44、55、66、で最後が77に到達します。真ん中で重複するのは33~44でこの間に7の倍数が出てくるのは35、42ですから2回切れているので3個が重複することになります。
したがって答えは17×2-3=31となります。
(2)は39と51ですからたがいに素ではありません。3で割ると13と17ですから、まず13と17の長方形について考えると1つの対角線は12+16+1=29です。
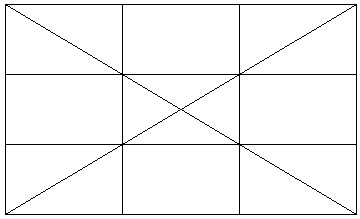
1本の対角線であれば29×3=87で答えが出るでしょう。
問題は真ん中です。そこで(1)と同じように考えます。正方形1辺の長さを13とすると17ずつ切っていきますから、17 34 51 68 85 102 119 136 153 170 187 204 で最後221に到達します。したがって真ん中は102~119です。この間に13の倍数は104 117と2つありますので、重複するのは3つです。したがって真ん中の長方形で切られている正方形は29×2-3=55ということになります。
すべての対角線が切る正方形は
29×4+55=116+55=171個となります。
==============================================================
田中貴.com通信を発刊しています。登録は以下のページからお願いします。
無料です。
田中貴.com通信ページ
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
親はどこまで教える?
==============================================================









