渋谷幕張2010年の問題。
図1・図2のように、長方形ABCDの辺CD上に点Eがあります。点Aと点Eを直線でつなぎ、AE上にFE=FBとなるような点Fをとると、AEとFBは直角に交わりました。このとき、次の問いに応えなさい。
(1)図1のように、FC=5㎝のとき、四角形BCEFの面積は何㎝2ですか。
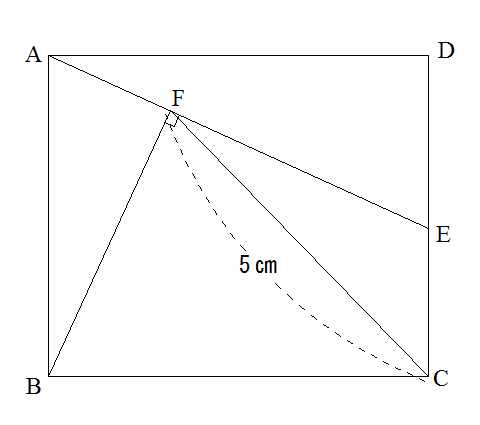
(2)図2のように、AF=2㎝ FE=4㎝のとき、四角形ABCDの面積は何㎝2ですか。
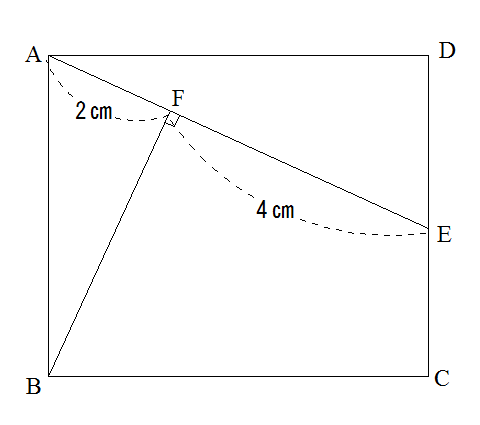
最近、こんな問題が増えてきています。発想が出てくるか、という感じはしますが、二等辺三角形だから同じ辺がわかっている。だからこの図形を動かしてみたら、という発想が出ればいいのですが。
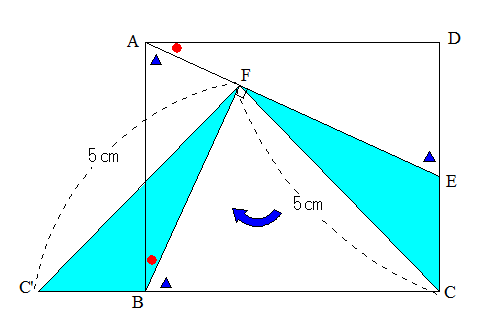
赤●の角度、青△の角度は図のようになりますので、そうなると三角形ACEを図のように移すことができる。
そうなると、一目瞭然というか。四角形BCEFの面積は1辺が5㎝の二等辺三角形の面積に等しいことになります。
したがって5×5÷2=12.5㎝2というのが答えになります。
(2)は、こちらの方がよほど簡単かもしれません。
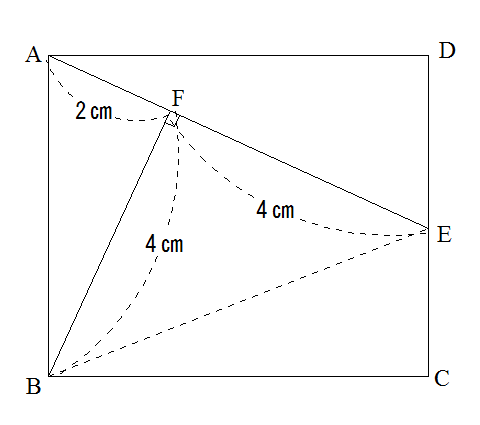
という図になるので、四角形ABCDの面積は三角形ABEの2倍になればいい。
したがって
(2+4)×4÷2×2=24㎝2
ということになるわけですが。
こういう、アイデアも、持っておきましょう。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
しつけとセルフコントロール
==============================================================
中学受験 算数オンライン塾
5月23日の問題
==============================================================









