2011年駒場東邦の問題。
ある正方形ABCDがあり、辺BC、CDのまん中の点をそれぞれM、Nとします。AとM、AとN、MとNを結んだ直線で正方形を折ると四面体をつくることができます。その時、四面体の体積は3087cm3でした。
(1)四面体をつくったとき、点Bと重なる点をすべて答えなさい。
(2)この正方形の1辺の長さを求めなさい。
(3)四面体をつくったとき、三角形AMNを底面としたときの、四面体の高さを求めなさい。
この形は覚えておくと良いでしょう。
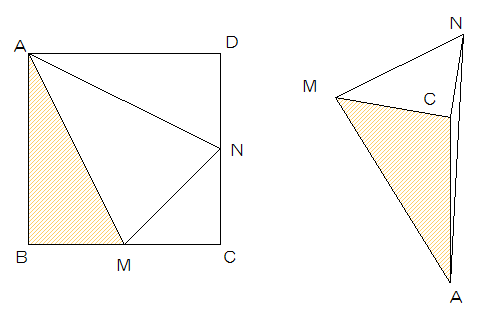
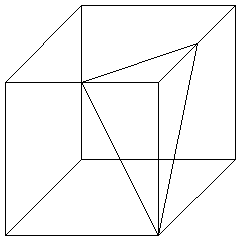
このように折ると、右図のような立体になります。
オレンジの面が同じです。
これは底面が直角三角形の三角すいで、立方体から切り取った立体です。
さて、(1)ですが、
BはCと重なりますが、DもCの位置にくるのを忘れないでください。
(答え)C、D
(2)図から立体のACの長さは正方形の1辺の長さになります。
その長さをXとすると、立体の体積は
1/2 × X × 1/2 × X × 1/2 × X × 1/3 = 1/24 × X × X × X = 3087
なんだ、三次方程式か、いえ、素数分解です。
3087=3×1029
1029は何で割れるか、1の位が9なので、7か17ぐらいはどうだろうか。 というので7で割ってみると
1029=7×147
ということになって、これは3×7×7×7
すると3087=3×3×7×7×7 これに24をかけると24=2×2×2×3ですから
X × X × X = 2×2×2×3×3×3×7×7×7=42×42×42
となるので、1辺の長さは42cmです。
(答え)42cm
(3)まず三角形AMNを計算しましょう。
42×42ー42×21×1/2×2ー21×21×1/2=42×21-10.5×21=31.5×21
でここまでで計算をやめます。
体積は3×3×7×7×7ですから
31.5×21×高さ×1/3 =3×3×7×7×7
31.5×21×高さ=3×3×3×7×7×7
高さ=3×3×7×7÷31.5=3×3×7×7×2÷63=7×2=14㎝
で答えは14㎝です。上手に計算してください。
(答え)14㎝
この形はたまに出題されますので、覚えておいた方が良いでしょう。
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
塾のやり方がすべてではない
==============================================================
中学受験 算数オンライン塾
7月24日の問題
==============================================================









