2010年甲陽学院の問題です。
4つの地点A、B、C、Dが10kmおきにこの順で並んでいます。車【1】はA地点からD地点に、車【2】と車【3】はD地点からA地点に向かいます。車【1】【2】【3】の速さはそれぞれ時速40km、50km、60kmです。B地点とC地点の間は車がすれ違うことができないので、対向車がB地点とC地点の間にいるとき、車【1】はB地点で、車【2】【3】はC地点で待たなければなりません。
車【2】は9時ちょうどに、車【3】は9時15分にそれぞれD地点を出発します。車の長さは考えず走っているときは常に一定の速さで走るものとします。
(1)9時ちょうどに車【1】がA地点を出発すると、車【3】がA地点に着くのは何時何分ですか。
(2)車【1】がB地点で待つことなく走るには、9時何分と9時何分の間にA地点を出発すればよいですか。ただし、9時から9時30分の間の時間で答えなさい。
(3)車【2】と【3】が同時にA地点に到着するには、車【1】は何時何分にA地点を出発すればよいですか。
(1)
車【1】は10÷40×60=15分 車【2】は10÷50×60=12分 車【3】は10÷60×60=10分で10kmを移動します。
車【2】が9時12分にCに到着し、車【1】は9時15分にBに到着するので、車【2】がBに到着するまで車【1】はBで待ちます。
一方車【3】は9時15分にDを出て、9時25分にCに到着しますので、車【1】がCに到着するまで待たなければなりません。
車【2】は9時24分にBに到着するので、車【1】はBを9時24分に出発、9時39分にCに到着します。
したがって車【3】は9時39分にCを出発し、20分でAに到着しますから、車【3】がAに到着するのは9時59分になります。
その動きをグラフに表すと以下のようになります。
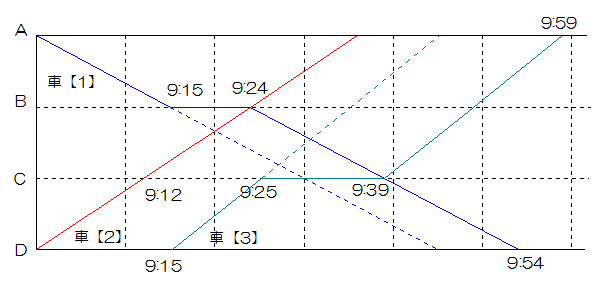
(答え)9時59分
(2)グラフから車【2】がBに到着するのは9時24分、車【3】がCに到着するのは9時25分ですから、この間に車【1】がBにつけば待つことはありません。
したがって9時24分ー15分=9時9分~10分の間に出発すればよいことになります。
(答え)9時9分~9時10分
(3)車【2】はDからAまで36分 車【3】はDからAまで30分で到着します。
車【2】はAに到着するのは、9時36分 車【3】は9時45分ですから、車【2】を9分間待たせれば良いことになります。
つまり9時12分+9分=9時21分にCを出発すると、9時33分にBを通過。すでに車【1】は通過しているため、車【3】は待つことなく9時25分にCを通過します。
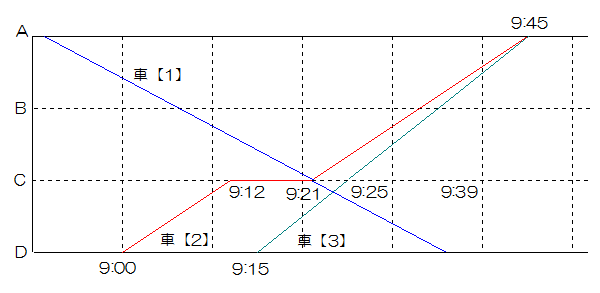
したがって車【1】がAを出発するのは9時21分ー15分×2=8時51分
(答え)8時51分
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
お試し受験は必要か?
==============================================================
今日の慶應義塾進学情報
動く歩道の問題
==============================================================

==============================================================
お知らせ
算数4年後期第14回 算数オンライン塾「場合の数(1)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








