2012年慶應湘南の問題です。
正六角形ABCDEFの辺BC、DE、FAのそれぞれまん中の点をP、Q、Rとし、辺AB、CD、EF上にそれぞれS、T、Uをとり、図のように結んで六角形PTQURSを作る。この六角形PTQURSと正六角形ABCDEFの面積の比を、最も簡単な整数の比で表しなさい。
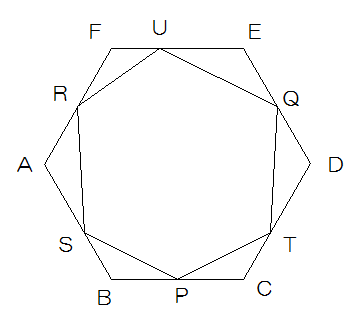
正六角形の問題は増えてきていますが、結局どう切ってどう組み合わせるか、ということがポイントになります。正六角形は同じ正三角形6枚が組み合わさってできる図形なので、その正三角形と同じ面積の三角形に分けていくことで問題の解法が見つかっていくことが多いのです。
STUはどこにおいてもよいので、中点においてしまいましょう。その方がわかりやすくなります。
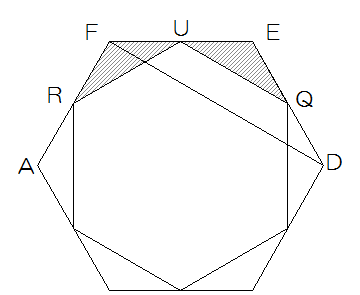
実際にはRとQが中点と決まっているのでUがEFの間のどこにあろうと斜線部の三角形の面積の合計は変わりません。
三角形EFDはこの正六角形の6分の1です。斜線の1つの三角形はその1/2×1/2=1/4
になるので1/6×1/4=1/24になりますが、これが6つあるので1/24×6=1/4
真ん中の六角形は1-1/4=3/4
したがって答えは3:4になります。
(答え)3:4
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
残った教材
==============================================================
今日の慶應義塾進学情報
慶應普通部 学校別対策の考え方(3)
==============================================================

==============================================================
お知らせ
算数5年前期第12回 算数オンライン塾「場合の数―順列―」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村







