早稲田高等学院2011年の問題です。
500gの太さが一様でない棒ABを用意しました。これに100gの皿と200gのおもりをつけて、Pでつるし、はかりをつくりました。図の状態で、はかりがつりあっているとき、次の問いに答えなさい。ただし、ひもの重さは考えないものとします。
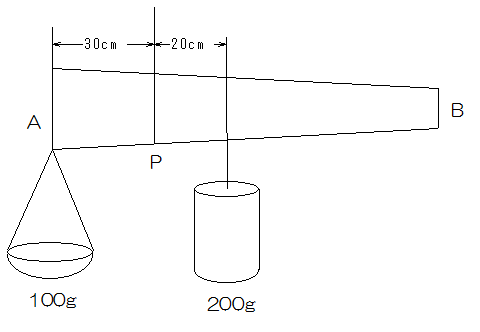
問1 棒ABの重心はAから何㎝のところにありますか。
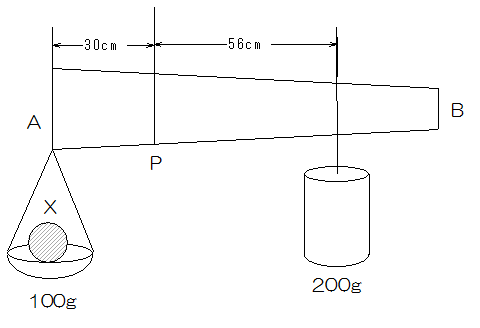
問2 このはかりは、おもりを右に動かすことで、皿にのせた物体が何gかを求めることができます。今、皿に物体Xをのせ、おもりを右に動かしたところ、図の状態でつりあいました。このときXは何gですか。
問1
Aにかかる回転力は支点をPとしたとき、100×30=3000になります。
一方おもりの方は200×20=4000ですから、おもりの方が多いので、Pよりも左側に重心があることがわかります。その差は4000-3000=1000で、棒の重さが500gですから
1000÷500=2㎝なので、Pの左側2cmのところに重心があります。
したがってAからは30-2=28cmです。
(答え)28cm
問2
Pの右側の回転力は200×56=11200
棒の重さの回転力は1000ですから11200-1000=10200
10200÷30=340gがXと皿の重さの合計になります。
したがってXの重さは340-100=240g
(答え)240g
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
レギュラーになれずとも
==============================================================
今日の慶應義塾進学情報
図形を折り返す問題
==============================================================

==============================================================
お知らせ
算数5年前期第12回 算数オンライン塾「場合の数―順列―」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








