売買損益算は割合を使って解く問題ですが、ことばが難しいので、まずその理解から勉強しましょう。
例えば、りんごを売るくだもの屋さんを考えます。りんごを売るためには、市場から買ってこなければなりません。その値段が1個50円だとします。この値段のことを仕入れ値(仕入れるとは売るために買ってくることをいいます。)とか原価といいます。
さて50円で買ってきたものを50円で売るともうけがありません。したがって商売をするのだから、これよりは高く売ることを考えます。
そこで1個について10円もうけようと考えました。これが利益です。仕入れ値と利益をたしたものがお客さんに売る値段ですから、定価(ていか)とか正価(せいか)という呼び方をします。
さてこの例では50円で買ってきたりんごに10円の利益を加えました。10円÷50円=0.2ですから、仕入れ値の2割の利益を加えて50円+10円=60円で定価をつけたことになります。
このことを2割増(2わリまし)といいます。2割増えたので、2割増ですが、もとが1で0.2増えたのですから掛け算で考えると1+0.2=1.2倍することになるのです。
50×1.2=60円で確かに定価に等しくなります。
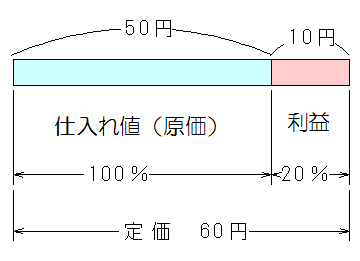
上の図で50円が原価(仕入れ値)です。これに10円の利益を加えて、定価にしました。利益は原価の20%にあたりますから、定価は原価の20%増しになります。
さてこのりんごが売れないので割引(わリびき)をしようと思います。割引というのは値段を安くすることをいいます。この例では60円の値段から10%安くすることを考えましょう。
10%は1割ですから1割引(いちわリびき)になります。1から0.1を引きますから1-0.1=0.9になります。
60×0.9=54円ですから、定価60円のものを1割引にすると54円です。
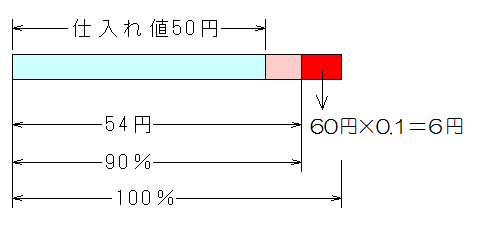
この例では仕入れ値(原価)が50円でしたので、まだ4円もうかることになるのです。
60円の1割は60×0.1 =6円ですから60-6=54円と計算しても求まりますが、最初から0.9倍するとした方が簡単でしょう。
(例題1)
次の( )にあてはまる数を答えなさい。
(1)定価200円の商品を2割引で売ると( )円で売ることになります。
(2)仕入れ値400円の商品を3割増で売ると( )円で売ることになります。
(解説と解答)
(1)
2割引とは0.2引くことですから1-0.2=0.8倍になります。2割引=0.8倍です。
200×0.8=160
(答え)160
(2)3割増とは0.3加えることですから1+0.3=1.3倍になります。3割増=1.3倍です。
400×1.3=520円
(答え)520
(例題2)
ある商品を1個600円で仕入れ、仕入れ値の4割増で定価をつけました。定価の2割引で売ると1個あたり、いくらもうかりますか。
(解説と解答)
600円で4割増ですから1.4倍します。600×1.4=840
840円の2割引ですから0.8倍します。840×0.8=672
672-600=72
(答え)72円
(例題3)
りんごを1個80円で100個仕入れました。いたんでいた10個は捨てて、仕入れ総額の3割5分の利益をみこんで定価をつけて売りました。このとき、1個の定価はいくらですか。
(解説と解答)
多少ややこしくなってきました。仕入れ総額というのは、仕入れた値段すべて、という意味ですから、80×100=8000円です。
いたんでいた10個を捨てましたから、残っているリンゴは90個です。仕入れ総額の3割5分の利益を出すのですから、8000×1.35=10800円の売り上げが必要になります。売り上げというのは、売れた値段の合計という意味です。
したがって1個あたりの定価は10800円÷90=120円となります。
(答え)120円
売買損益の問題は、まず言葉でひっかかります。あまり聞きなれない言葉をいろいろ使います。割引、定価、原価、利益、「もうかりました」などなど。したがって、実際に問題文を読みながら、その内容を理解することがまず大事です。さらに割合を使ったり、つるかめ算を使ったりなどいろいろ応用の範囲は広がっていきますが、問題文の内容をしっかり読み取って問題を解いていってください。
以下のプリントもお役立ていただければと思います。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
あえて予習をする必要があるのか?
==============================================================
中学受験 算数オンライン塾
4月14日の問題
==============================================================

==============================================================
お知らせ
算数5年前期第12回 算数オンライン塾「場合の数―順列―」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








