今週は場合の数の組み合わせについて考えます。
組み合わせは、順列の考え方を応用して計算します。すなわち順列を計算して、1つの組み合わせをいくつの順列としているか計算して割るのです。
例えばABCDの4人の中から3人を選ぶ組み合わせは、順列で考えると
4×3×2=24通りになります。
で、ABCという組み合わせは3×2×1=6通りで計算しているので、
24÷6=4通り となるわけです。4人の中から3人を選ぶ場合、残る1人の選び方は4通りですから、答えは4通りとわかりますが、組み合わせの公式はこのようにしてできています。
n個の中からr個を選ぶ組み合わせの公式は、
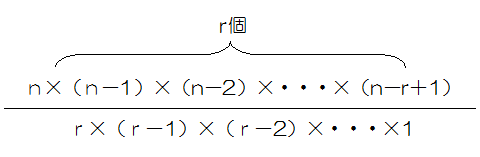
となっていますが、分子がn個の中からr個を選ぶ順列、分母が1つの組み合わせを何通りに順列に計算しているか、になっているわけです。
(例題1)
ABCDEFの6人がいます。これについて次の問いに答えなさい。
(1)4人の掃除当番を決める決め方は何通りありますか。
(2)2人の日直を決める決め方は何通りありますか。
(解説と解答)
(1)6人の中から4人を選ぶのですから、
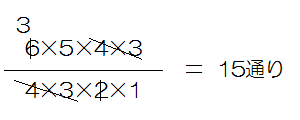
になります。
(2)同様に6人の中から2人を選ぶのですから、
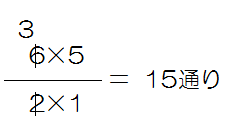
になります。
答えが同じになるのは偶然ではなく、これが同じ問題であるからです。4人の掃除当番を決めるということは、掃除当番でない2人を決めることと同じです。つまり6人の中から4人を決める組み合わせは6人の中から2人を決める組み合わせと同じことになるのです。
(例題2)
正十二角形の対角線の数を求めなさい。
(解説と解答)
それぞれの分野で公式がありますが、組み合わせの考え方から生まれた公式もあります。
正十二角形には12個の点があります。その1つの点からは自分と両隣を引いた9個(12-3=9)の点に対して対角線を引くことができます。ただしAからBとBからAは同じ対角線ですから1つの対角線を2本で計算することになるので、
12×(12-3)÷2=54本になります。
(例題3)
オリンピックのサッカーでは16か国が参加します。16か国を4つのグループに分けて総当たり戦を行います。その結果、上位2チームが決勝トーナメントを行い、1位から3位までを決めます。3位決定戦を含めて試合数は全部で何試合ありますか。
(解説と解答)
1つのグループは16÷4=4か国ですから、組み合わせは4×3÷2=6試合あります。したがって4つのグループでの試合数は6×4=24試合。
上位2チームが決まって4グループで決勝トーナメントに参加する国は2×4=8か国。トーナメントは勝ち抜き戦ですから、1試合で必ず1チームが負けます。金メダルのチームだけが負けないので、決勝トーナメントの試合数は8-1=7試合。
これに3位決定戦が1試合加わるので合計8試合。
したがって試合数は全部で24+8=32試合になります。
(答え)32試合
(例題4)
以下の図の中に四角形は何通りありますか。

(解説と解答)
1つの四角形はたての線2本、横の線2本で決まります。たての線は4本あるので、組み合わせは4×3÷2=6通り 横の線は3本あるので、組み合わせは3×2÷2=3通りですから、四角形は全部で
6×3=18個あります。
別の考え方で検証してみましょう。
1つの正方形でできている四角形は6個。
2つの正方形を横に並べてできる四角形は4個
2つの正方形をたてに並べてできる四角形は3個
3つの正方形を横に並べてできる四角形は2個
4つの正方形を並べてできる四角形は2個
6つの正方形を並べてできる四角形は1個
ですから、合計6+4+3+2+2+1=18個
になります。
(答え)18個
(例題5)
なしが3個、みかんが2個、りんごが2個あります。この中から3つを選んでジュースをつくります。ジュースのつくり方は何通りありますか。
(解説と解答)
これはやや面倒な問題です。
なし3個の中では区別がつきませんから、単純に公式を使うわけにはいきません。
なし、なし、なし、
なし、なし、みかん、なし、なし、りんご
なし、みかん、みかん、なし、みかん、りんご、なし、りんご、りんご、
みかん、みかん、りんご、 みかん、りんご、りんご
となるわけですが、ここで気を付けなければいけないのは、同じ組み合わせを排除するルールを作っておくことです。
一番上はなしが3個、2番目はなしが2個、3番目はなしが1個、4番目はなしを使わない場合で分けています。
またなしを最初にかき、つぎにみかんを書き、りんごを最後に書くので、りんごの右になしやみかんが出てこないようにします。
こうすることで重複をせずに書き出すことができるでしょう。
(答え)8通り
組み合わせはこのように、公式だけでできる問題ばかりではありません。場合を分けたり、条件を整理して書き出すなどの作業が必要になる問題の方がむしろ多いので、重複を許さないような書き方を工夫していかなければなりません。書き出すこともいとわず、むしろ整理してきちんと作業できるようにしっかり練習していきましょう。
以下のプリントもお役立ていただければと思います。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
馴染める学校を選ぶ
==============================================================
中学受験 算数オンライン塾
5月26日の問題
==============================================================

==============================================================
お知らせ
算数5年前期第18回 算数オンライン塾「旅人算とグラフ(1)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








