2013年、浦和明の星の問題です。
図1は、底面が半径3cmの円で、高さが12cmの円柱であり、(ア)と(イ)を結んでできる直線は底面に垂直です。また、図2はABの長さが12cm、角Bが直角である三角形の形をした紙です。いま、この紙をA、Bがそれぞれ円柱の(ア)、(イ)のの部分に重なるようにして巻きつけたところ、3周して、Cがちょうど(イ)のところにきました。
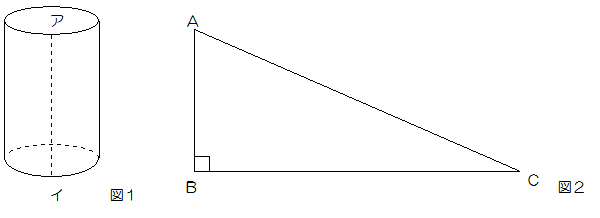
紙を巻きつけた状態で円柱全体に色をぬり、その後この紙を円柱からはずしました。このとき、三角形の形をした紙の.色がついた部分の面積を求めなさい。ただし、円周率は3.14とします。
(解説と解答)
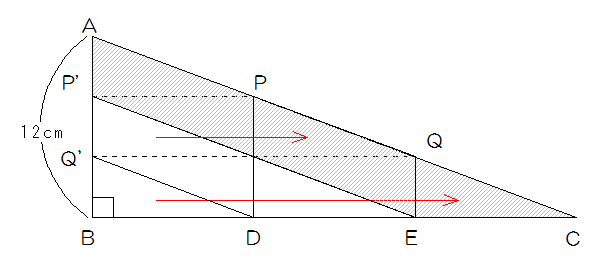
ちょうど3周分巻きついたので、BCの長さは円柱の底面の円の円周の3倍の長さになります。
BCの長さを3等分して、図のようにBD=DE=ECとするとP点はP’に行き、QはQ’に行くので、巻きついた紙を上からぬると、図の斜線部分になります。
AP’=P’Q’=Q’Bですから、斜線部分は三角形ABCの1-2/3×2/3=5/9になります。
BCの長さは3×2×3.14×3=18×3.14ですから三角形ABCの面積は12×18×3.14÷2=108×3.14になるので、
108×3.14×5/9=60×3.14=188.4cm2になります。
(答え)188.4cm2
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
ミスはなくならない?
==============================================================
今日の慶應義塾進学情報
サウナはなぜやけどしない?
==============================================================

==============================================================
お知らせ
算数5年前期第19回 算数オンライン塾「旅人算とグラフ(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








