今回は旅人算とグラフの1回目です。
旅人算とは速さの問題の中で、追いつく場所や出会う場所、あるいはそれにかかる時間を求める問題です。速さはのちに比を使いこなすことによって、簡単に解くことができるようになりますが、旅人算の考え方で入試問題はある程度解きこなせるように作られています。
したがってこの基本はしっかり身に付けて、さらに応用問題に利用していきましょう。
(例題1)1200m離れたAとBがあります。Aから太郎君が、Bから次郎君が向かい合って同時に出発しました。太郎君の分速は120m、次郎君の分速は80mです。二人が出会うのは出発してから何分後で、それはAから何mのところですか。
(解説と解答)
基本です。二人が向かい合うのですから、二人の速さの和で近づいていきます。したがって
1200÷(120+80)=6分後に出会うことになり、それはAから120×6=720mのところになります。
(答え)6分後 720m
(例題2)
太郎君は分速が80m、次郎君は分速が100mです。太郎君が出発して6分後に次郎君が出発して太郎君を追いかけました。次郎君が太郎君に追いつくのは太郎君が出発してから何分後ですか。
(解説と解答)
この場合はまず太郎君が6分進みます。80×6=480m進むので、この差をつめていきます。
1分あたり、次郎君は太郎君より100-80=20m速いので、480÷20=24分後。
ここでミスが出がちです。
問題は太郎君が出発してから、と書いてありますので24+6=30分後になります。
(答え)30分後
(例題3)
太郎君がAからBへ、次郎君がBからAに同時に出発すると二人は12分後には出会います。AからBまで1200mです。太郎君は次郎君よりも分速が20m速いとすると、次郎君はBからAまで何分かかりますか。
(解説と解答)
最初の条件から二人の分速の和がわかります。1200÷12=100mです。
差が20mですから、和差算を使って(100+20)÷2=60mが太郎君の分速、100-60=40mが次郎君の分速になるので1200÷40=30分、次郎君はBからAまでかかります。
(答え)30分
(例題4)
太郎君がAからBへ、次郎君がBからAで同時に出発しました。グラフは二人がそれぞれ出発してからの時間を示しています。
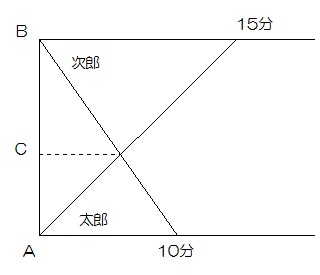
AからBまで3000mのときAからCまでの距離を求めなさい。
(解説と解答)
問題の条件がグラフによって提示されることもあります。これは簡単な例ですが、太郎君がAからBまで15分かかり、次郎君はBからAまで10分かかることがわかります。またCは二人が出会った場所になります。
3000÷15=200m・・・太郎君の分速
3000÷10=300m・・・次郎君の分速
3000÷(200+300)=6分後に二人は出会うので、A~Cまでの距離は200×6=1200mになります。
(答え)1200m
(例題5)
太郎君がAを出発してから10分後に次郎君が自転車で太郎君を追いかけました。
グラフはその時の二人のようすをしめしたものです。
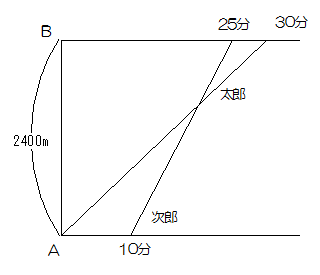
次郎君が太郎君に追いついたのは次郎君が出発してから何分後ですか。
(解説と解答)
この問題はグラフで追い越しを考えています。AからBまでの距離がグラフに表示されています。
2400÷30=80m・・・太郎君の分速
2400÷(25-10)=160m・・・次郎君の分速
次郎君が出発するとき、太郎君は10分移動しているので
80×10=800m先にいますから、800÷(160-80)=10分後に追いつきます。
(答え)10分後
(例題6)
太郎君と次郎君がAを同時に出発してAB間を一往復しました。二人が出会ったのは出発して12分後で、Aから1200mのところでした。AからBまで2400mあるとき、次の問いに答えなさい。ただし太郎君の方が次郎君より速く歩きます。
(1)太郎君の分速を求めなさい。
(2)太郎君がBで折り返したとき、速さを半分にすると二人が出会うのはAから何mのところですか。
(解説と解答)
(1)二人の動きを図にすると下図のようになります。
赤い線が次郎君、青い線が太郎君です。
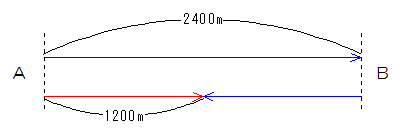
二人は出会うまでの間に合わせて2400×2=4800m移動しなければなりません。次郎君が移動したのは1200mですから太郎君は4800-1200=3600m移動するので
3600÷12=300mが太郎君の分速です。
(答え)300m
(2)太郎君は分速が300mなのでBに到着するのは2400÷300=8分後です。
次郎君の分速は1200÷12=100mですから、100×8=800m次郎君は動いています。
したがって二人の間の距離は2400-800=1600mです。
太郎君がここで速さを半分にすると300÷2=150mですから、二人の速さの和は
100+150=250mになるので。
1600÷250=6.4分後に二人が出会います。次郎君は8+6.4=14.4分動いているのでその場所はAから100×14.4=1440mになります。
(答え)1440m
旅人算は速さの基本です。入試問題ではさらに条件が複雑になっていきますが、まずは追いつく場合、出会う場合をしっかり区別して解いていきましょう。
以下のプリントもお役立ていただければと思います。
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
初志貫徹(2)
==============================================================
今日の慶應義塾進学情報
気を回す必要はない
==============================================================

==============================================================
お知らせ
算数5年前期第20回 算数オンライン塾「まとめのテスト」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








