2009年白百合中学の問題です。
辺OAと辺OBの間の角度を60°とし、孤ACと孤CBを同じ長さとします。四角形EFCDは長方形です。次に辺EFの真ん中の点Mをとり、点Dと線で結びます。その辺DMと辺OCとが交わる点をHとし、辺GHの長さが2.4cmで、さらに辺ODと辺OEの長さの比が2:1であったとき、辺CFの長さを求めなさい。
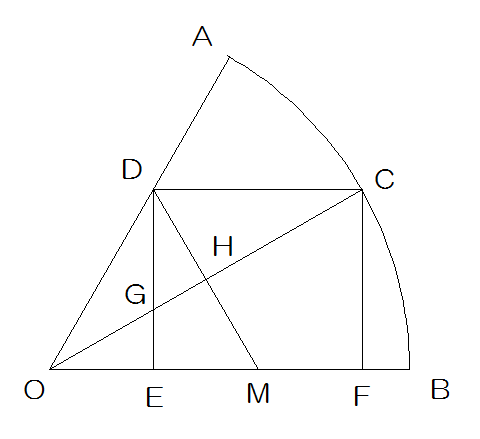
弧AC=弧CBですから角AOC=角COB=60÷2=30°
角DCO=角COB=30°から 三角形DOCはDO=DCの二等辺三角形になります。
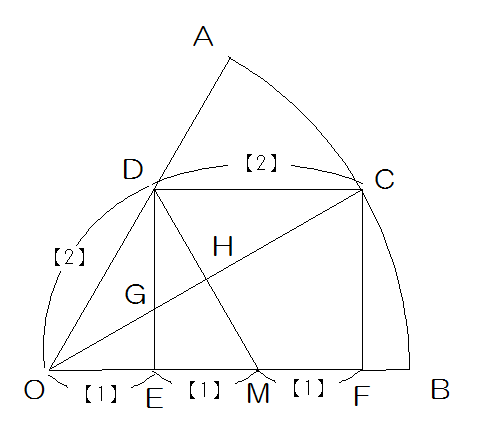
ODの長さを【2】とするとDC=【2】、OE=【1】
MがEFの中点ですから
EM=MF=【1】
三角形OGEと三角形DGCの相似よりOG:GC=1:2
三角形OHMと三角形DHCの合同よりOH:HC=1:1
したがって
OG:GH:HC=1:0.5:1.5=2:1:3
GH=2.4㎝よりOC=2.4×6=14.4㎝
三角形OCFも30°60°90°の三角形なのでOC:CF=2:1より
CF=14.4÷2=7.2
(答え)7.2cm
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
地図の問題をPDFで見る
==============================================================
中学受験 算数オンライン塾
10月16日の問題
==============================================================

==============================================================
お知らせ
算数4年後期第9回 算数オンライン塾「方陣算」をリリースしました。
詳しくはこちらから
==============================================================









