2009年晃華学園の問題です。
下の図1のように、辺ABと辺ACの長さが等しい直角二等辺三角形ABCと直角三角形BCDを合わせて、四角形ABDCを作りました。さらに、この四角形を下の図2のように2つの図形、台形ABDEと直角三角形ACEに分けたとき、次の問いに答えなさい。
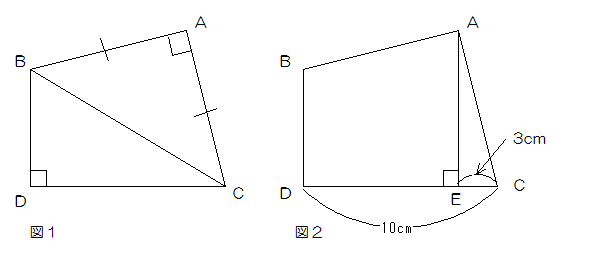
(1)台形ABDEの面積を求めなさい。
(2)直角二等辺三角形ABCの面積を求めなさい。
(1)図のように、三角形AECを三角形ABFに移します。
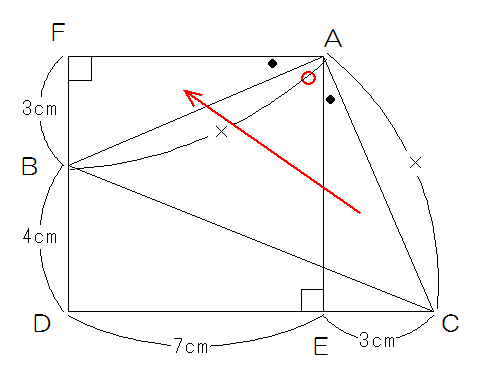
角BAC=90°ですから、角EAFも90°になり、三角形AFBと三角形AECは合同な三角形ですから、角AFBも90°で四角形AFDEは1辺が7cmの正方形です。
したがって台形ABDEの面積は7×7-3×7÷2=49-10.5=38.5cm2
(答え)38.5cm2
(2)BD=4cmですから。三角形BDCの面積は4×10÷2=20㎝2
したがって直角三角形ABCの面積は49-20=29
(答え)29cm2
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
集団指導と個別指導
==============================================================
中学受験 算数オンライン塾
6月11日の問題
==============================================================

==============================================================
お知らせ
算数5年前期第19回 算数オンライン塾「旅人算とグラフ(2)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================
![]()
にほんブログ村








