2012年市川中学の問題です。
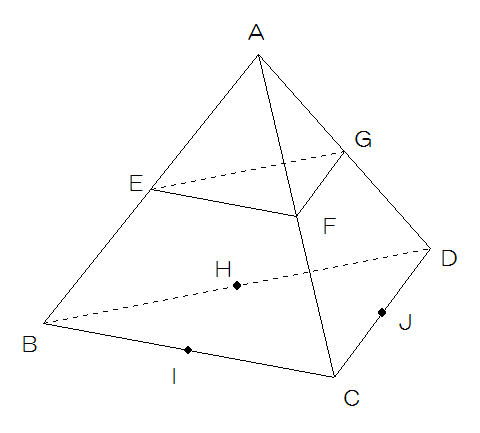
図のように、すべての麺が正三角形でできた三角すいABCDがあり、各辺のちょうど真ん中の点をそれぞれ、E、F、G、H、I、Jとします。
点Pは点Aを出発し三角すいABCDと正三角形EFGの辺上を動き、1回の移動で必ずとなりの点に動きます。たとえば、点BのとなりはE、H、Jです。
このとき、次の問いに答えなさい。
(1)点Pは、途中で同じ点を通ってはいけないものとして、ちょうど7回の移動ではじめて点Aに戻る動き方は全部で何通りありますか。
(2)点Pは、同じ点を何回通ってもよいものとして、ちょうど4回の移動で点Aに移動する動き方は何通りありますか。
(1)大きな正三角形(例えば三角形ABC)を1周するのには6回移動します。7回で戻るためには、大きな正三角形を例えば
A→E→B→H→C→Fと来て、これで5回ですから、FからGに行き、GからAに戻るという行き方が考えられます。
この場合大きな三角形の回り方はAからB、C、Dまで移動するので3通り。
そこから左右に分かれるので2通り。E、F、Gのどれかにもどったとき、片方には行けないのでAに戻るのは1通り。ですから、
3×2×1=6通りあります。
次に最初にA→G→Fと来て、その反対に回る方法は
AからE、F、Gのどれかに行くので3通り。次に左右に分かれて2通り。Aに戻る大きな三角形の回り方は1通りですから、これも
3×2×1=6通りあります。
AからB、C、Dまで下りてしまうと三角形BCDのどれかに行かねばならず、ここで4回移動します。ここから3回で戻る方法は、これ以外にはありません。
またAからE、F、Gに降りて下に降りず、横に移動すれば、ここで2回移動するので、残り5回で移動しますが、これもここでB、C、Dのどれかに降りてしまわないと、5回では戻れません。
したがって、これ以外にないので、答えは12通りです。
(答え)12通り
(2)
まずE、F、Gへ一往復し、もう一度E、F、Gを一往復する方法があるので、これが3×3=9通り
次にB、C、Dまで下りると来た道を戻るしか方法がないので、これが3通り。
次にAからEに降りてF、Gと通ってAに戻る方法があり、これは最初がE、F、Gの3通り。次が2通りで、もどることもできるから、その次も2通りあり、合計では3×2×2=12通り
したがって合計は9+3+12=24通り
(答え)24通り
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
早とちり
==============================================================
今日の慶應義塾進学情報
慶應だけ受ける
==============================================================

==============================================================
お知らせ
算数5年後期第8回 算数オンライン塾「平面図形と比(3)」をリリースしました。
詳しくはこちらから
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村








